Difference between revisions of "Separation Logic"
| (11 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
CVC4 supports a syntax for separation logic as an extension of the *.smt2 language. | CVC4 supports a syntax for separation logic as an extension of the *.smt2 language. | ||
| − | =Signature | + | =Signature= |
| − | Given a base theory T, CVC4 | + | Given a (decidable) base theory T, CVC4 has a [http://homepage.divms.uiowa.edu/~ajreynol/atva16.pdf decision procedure] for quantifier-free <math>SL(T)_{Loc,Data}</math> formulas, where "Loc" and "Data" are any sort belonging to T. |
| − | A SL(T)_{Loc,Data} formula is one from the following grammar: | + | A <math>SL(T)_{Loc,Data}</math> formula is one from the following grammar: |
F : L | (emp t u) | (pto t u) | (sep F1 ... Fn) | (wand F1 F2) | ~F1 | F1 op ... op Fn | F : L | (emp t u) | (pto t u) | (sep F1 ... Fn) | (wand F1 F2) | ~F1 | F1 op ... op Fn | ||
where "op" is any classical Boolean connective, t and u are terms built from symbols in the signature of T of sort Loc and Data respectively, and L is a T-literal. | where "op" is any classical Boolean connective, t and u are terms built from symbols in the signature of T of sort Loc and Data respectively, and L is a T-literal. | ||
| Line 10: | Line 10: | ||
the operator "sep" denotes separation start and is variadic, and the operator "wand" denote magic wand. | the operator "sep" denotes separation start and is variadic, and the operator "wand" denote magic wand. | ||
| − | The semantics of | + | =Semantics= |
| + | |||
| + | A satisfiability relation <math>I,h \models_{SL} \varphi</math> is defined for <math>SL(T)_{Loc,Data}</math> formulas <math>\varphi</math>, | ||
| + | where I is an interpretation, and h is a heap. The semantics of separation logic operators are as follows: | ||
{| class="wikitable" cellpadding="5" border="0" style="border-collapse:collapse" | {| class="wikitable" cellpadding="5" border="0" style="border-collapse:collapse" | ||
| Line 16: | Line 19: | ||
| <math>I,h \models_{SL} </math> L | | <math>I,h \models_{SL} </math> L | ||
| Iff | | Iff | ||
| − | | <math>I \models</math> L, if L is a | + | | <math>I \models</math> L, if L is a T-literal |
|- | |- | ||
| − | | <math>I,h \models_{SL}</math> (emp t u) | + | | <math>I,h \models_{SL}</math> (emp <math>t \ u</math>) |
| Iff | | Iff | ||
| <math>h = \emptyset</math> | | <math>h = \emptyset</math> | ||
|- | |- | ||
| − | | <math>I,h \models_{SL}</math> (pto t u) | + | | <math>I,h \models_{SL}</math> (pto <math>t \ u</math>) |
| Iff | | Iff | ||
| <math>h = \{(t^I,u^I)\} \text{ and } t^I\not=nil^I</math> | | <math>h = \{(t^I,u^I)\} \text{ and } t^I\not=nil^I</math> | ||
| Line 28: | Line 31: | ||
| <math>I,h \models_{SL} </math> (sep <math>\phi_1 \ldots \phi_n</math>) | | <math>I,h \models_{SL} </math> (sep <math>\phi_1 \ldots \phi_n</math>) | ||
| Iff | | Iff | ||
| − | | there exist heaps <math>h_1,\ldots,h_n</math> s.t. <math>h=h_1\uplus \ldots \uplus | + | | there exist heaps <math>h_1,\ldots,h_n</math> s.t. <math>h=h_1\uplus \ldots \uplus h_n</math> and <math>I,h_i \models_{SL} \phi_i, i = 1,\ldots,n</math> |
|- | |- | ||
| − | | <math>I,h \models_{SL}</math> (wand <math>\phi_1 \phi_2</math>) | + | | <math>I,h \models_{SL}</math> (wand <math>\phi_1 \ \phi_2</math>) |
| Iff | | Iff | ||
| for all heaps <math>h'</math> if <math>h'\#h</math> and <math>I,h' \models_{SL} \phi_1</math> then <math>I,h'\uplus h \models_{SL} \phi_2</math> | | for all heaps <math>h'</math> if <math>h'\#h</math> and <math>I,h' \models_{SL} \phi_1</math> then <math>I,h'\uplus h \models_{SL} \phi_2</math> | ||
|} | |} | ||
| − | + | where <math>h_1 \uplus \ldots \uplus h_n</math> denotes the disjoint union of heaps <math>h_1, \ldots, h_n</math> and | |
| − | + | <math>h'\#h</math> denotes that heaps h' and h are disjoint, and <math>nil</math> is a distinguished variable of sort Loc. | |
| − | + | All classical Boolean connectives are interpreted as expected. | |
| − | + | Note that the arguments of "emp" are used to denote the type of the heap and have no meaning otherwise. | |
| − | + | ||
| − | + | ||
| − | + | ||
=Syntax= | =Syntax= | ||
| Line 58: | Line 58: | ||
| Empty heap | | Empty heap | ||
| <code>N/A</code> | | <code>N/A</code> | ||
| − | | <code>('''emp''' | + | | <code>(_ '''emp''' T1 T2)</code> |
| − | | <code>em.mkExpr('''kind::SEP_EMP''', X, Y);</code> | + | | <code>em.mkExpr('''kind::SEP_EMP''', X, Y);</code> where X and Y are of type T1 and T2. |
|- | |- | ||
| Points-to | | Points-to | ||
| Line 92: | Line 92: | ||
(assert (and (pto x a) (pto x b))) | (assert (and (pto x a) (pto x b))) | ||
(assert (not (= a b))) | (assert (not (= a b))) | ||
| + | (check-sat) | ||
| + | |||
| + | The following input on heaps U -> Int is satisfiable. Notice that the formula (not (emp x 0)) is satisfied by heaps U -> Int (the types of x and 0 respectively) whose domain is non-empty. | ||
| + | (set-logic QF_ALL_SUPPORTED) | ||
| + | (set-info :status unsat) | ||
| + | (declare-sort U 0) | ||
| + | (declare-const x U) | ||
| + | (declare-const a Int) | ||
| + | (assert (and (not (_ emp Int U)) (pto x a)) | ||
(check-sat) | (check-sat) | ||
| Line 103: | Line 112: | ||
(assert (pto x (node 0 y z))) | (assert (pto x (node 0 y z))) | ||
(check-sat) | (check-sat) | ||
| + | |||
| + | Given a separation logic input, | ||
| + | the sorts Loc and Data are inferred by CVC4, and must be consistent across all predicates occurring in an input. CVC4 does not accept an input such as: | ||
| + | (set-logic QF_ALL_SUPPORTED) | ||
| + | (declare-sort U 0) | ||
| + | (declare-const x U) | ||
| + | (assert (and (pto x 0) (pto 1 2))) | ||
| + | since the sorts of the first arguments of the points-to predicates do not agree. | ||
Latest revision as of 08:59, 2 August 2018
CVC4 supports a syntax for separation logic as an extension of the *.smt2 language.
Contents
Signature
Given a (decidable) base theory T, CVC4 has a decision procedure for quantifier-free 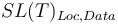 formulas, where "Loc" and "Data" are any sort belonging to T.
A
formulas, where "Loc" and "Data" are any sort belonging to T.
A 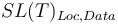 formula is one from the following grammar:
formula is one from the following grammar:
F : L | (emp t u) | (pto t u) | (sep F1 ... Fn) | (wand F1 F2) | ~F1 | F1 op ... op Fn
where "op" is any classical Boolean connective, t and u are terms built from symbols in the signature of T of sort Loc and Data respectively, and L is a T-literal. The operator "emp" denotes the empty heap constraint, the operator "pto" denotes the points-to predicate, the operator "sep" denotes separation start and is variadic, and the operator "wand" denote magic wand.
Semantics
A satisfiability relation 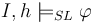 is defined for
is defined for 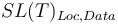 formulas
formulas 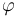 ,
where I is an interpretation, and h is a heap. The semantics of separation logic operators are as follows:
,
where I is an interpretation, and h is a heap. The semantics of separation logic operators are as follows:
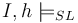 L L
|
Iff | 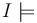 L, if L is a T-literal L, if L is a T-literal
|
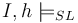 (emp (emp 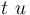 ) )
|
Iff | 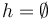
|
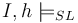 (pto (pto 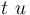 ) )
|
Iff | 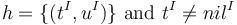
|
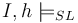 (sep (sep  ) )
|
Iff | there exist heaps  s.t. s.t. 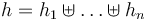 and and 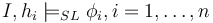
|
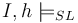 (wand (wand 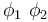 ) )
|
Iff | for all heaps 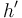 if if 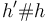 and and 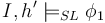 then then 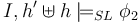
|
where  denotes the disjoint union of heaps
denotes the disjoint union of heaps  and
and
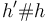 denotes that heaps h' and h are disjoint, and
denotes that heaps h' and h are disjoint, and 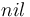 is a distinguished variable of sort Loc.
All classical Boolean connectives are interpreted as expected.
Note that the arguments of "emp" are used to denote the type of the heap and have no meaning otherwise.
is a distinguished variable of sort Loc.
All classical Boolean connectives are interpreted as expected.
Note that the arguments of "emp" are used to denote the type of the heap and have no meaning otherwise.
Syntax
Separation logic in CVC4 requires the "all supported" logic:
(set-logic QF_ALL_SUPPORTED)
The syntax for the operators of separation logic is summarized in the following table:
| CVC language | SMTLIB language | C++ API | |
|---|---|---|---|
| Empty heap | N/A
|
(_ emp T1 T2)
|
em.mkExpr(kind::SEP_EMP, X, Y); where X and Y are of type T1 and T2.
|
| Points-to | N/A
|
(pto X Y)
|
em.mkExpr(kind::SEP_PTO, X, Y);
|
| Separation star | N/A
|
(sep C1 ... Cn)
|
em.mkExpr(kind::SEP_STAR, C1, ..., Cn);
|
| Magic wand | N/A
|
(wand C1 C2)
|
em.mkExpr(kind::SEP_WAND, C1, C2);
|
| Nil element | N/A
|
(as nil T)
|
em.mkUniqueVar(T,kind::SEP_NIL);
|
Examples
The following input on heaps Int -> Int is unsatisfiable:
(set-logic QF_ALL_SUPPORTED) (set-info :status unsat) (declare-const x Int) (declare-const a Int) (declare-const b Int) (assert (and (pto x a) (pto x b))) (assert (not (= a b))) (check-sat)
The following input on heaps U -> Int is satisfiable. Notice that the formula (not (emp x 0)) is satisfied by heaps U -> Int (the types of x and 0 respectively) whose domain is non-empty.
(set-logic QF_ALL_SUPPORTED) (set-info :status unsat) (declare-sort U 0) (declare-const x U) (declare-const a Int) (assert (and (not (_ emp Int U)) (pto x a)) (check-sat)
The following input on heaps Int -> Node is satisfiable, where Node denotes a user-defined inductive datatype:
(set-logic QF_ALL_SUPPORTED) (set-info :status sat) (declare-const x Int) (declare-const y Int) (declare-const z Int) (declare-datatypes () ((Node (node (data Int) (left Int) (right Int))))) (assert (pto x (node 0 y z))) (check-sat)
Given a separation logic input, the sorts Loc and Data are inferred by CVC4, and must be consistent across all predicates occurring in an input. CVC4 does not accept an input such as:
(set-logic QF_ALL_SUPPORTED) (declare-sort U 0) (declare-const x U) (assert (and (pto x 0) (pto 1 2)))
since the sorts of the first arguments of the points-to predicates do not agree.
