Tutorials
CVC language
<coming soon...>
Finding these examples
Except where noted below, tutorial code appearing in this section is kept in the examples/cvc directory of the CVC4 source distribution. However, tutorial material on this page might be more recent than your CVC4 download. Please refer to the most recent nightly build for the most recent tutorial code.
SMT-LIB
We recommend David Cok's excellent tutorial on SMT-LIB. When running examples from this tutorial, we recommend using CVC4's --smtlib-strict command line option, which enters a stricter compliance mode.
CVC4 should be compliant with the standard, and thus also with David Cok's tutorial, except for some unsupported functionality as noted in the SMT-LIB compliance section of this wiki. If you find something that you believe to be nonconformant, please report it as a bug.
C++ API
- helloworld : a simple example to start off with
- linear_arith : real and integer linear arithmetic
- combination : integer and uninterpreted function example
- bitvectors : bit-vectors example
- bitvectors_and_arrays : integer and uninterpreted function example
- quantifiers
- strings : strings example
Finding and compiling these examples
Except where noted below, tutorial code appearing in this section is kept in the examples/api directory of the CVC4 source distribution. However, tutorial material on this page might be more recent than your CVC4 download. Please refer to the most recent nightly build for the most recent tutorial code.
To compile everything in the examples/ directory, you can issue the command make examples from the top-level of the source distribution. This will first build CVC4 (if it isn't already built) and then the examples. Some examples from the directory may not be compiled, if (for instance) you haven't built with support for Java, or if you haven't built with support for the compatibility interface; however, all native C++ API examples should be, and those are the only ones appearing in this section.
Note that the example API code in the examples/ directory is intended to be compiled and linked against a CVC4 library built from the source tree. If you try to compile them yourself, against a CVC4 library installed (for example) in /usr, you may find that certain headers cannot be found. There is an easy fix. CVC4 #includes like the following:
#include "expr/expr.h"
should be rewritten to this form:
#include <cvc4/expr/expr.h>
or, most likely, you can remove all such #includes and replace with this single one:
#include <cvc4/cvc4.h>
The example code is not installed by make install.
helloworld
To get used to CVC4, let us go through the following example line-by-line:
#include <iostream>
#include <cvc4/cvc4.h>
using namespace CVC4;
int main() {
ExprManager em;
Expr helloworld = em.mkVar("Hello World!", em.booleanType());
SmtEngine smt(&em);
std::cout << helloworld << " is " << smt.query(helloworld) << std::endl;
return 0;
}
(The example can be found in examples/api/helloworld.cpp.)
First we include the standard <iostream> library, and next we include the public interface for CVC4:
#include <cvc4/cvc4.h>
cvc4/cvc4.h includes definitions for all of the classes we'll need including ExprManager, Expr and SmtEngine. All of CVC4 lives in the namespace CVC4 and to save a bit of typing let's use the namespace. Now construct a new ExprManager named em.
ExprManager em;
ExprManagers are in charge of constructing and managing symbolic expressions in CVC4. We then construct the expression Expr helloworld.
Expr helloworld = em.mkVar("Hello World!", em.booleanType());
helloworld is a symbolic variable with the name "Hello World!" and the type boolean. Note that we ask em to both make the variable and to get em.booleanType(). We now make the main driver for CVC4 reasoning the SmtEngine smt using em as its ExprManager.
SmtEngine smt(&em);
Finally we print helloworld and query the SmtEngine if the boolean variable helloworld is valid.
std::cout << helloworld << " is " << smt.query(helloworld) << std::endl;
We can compile the program helloworld from helloworld.cpp by linking against -lcvc4
$ g++ helloworld.cpp -o helloworld -lcvc4 $ ./helloworld Hello World! is invalid
This should all work if libcvc4 was installed using make install. If you used make install to a non-standard location, look at instructions for using non-standard prefix. If you insist on not-using make, look at instructions for Build_Problems#libcvc4_without_make_install.
linear_arith
With helloworld under our belt, let's try to work through the more advanced examples/api/linear_arith.cpp . In this example, we'll try to show that for 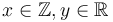 if
if 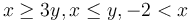 then
then 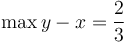 .
We can do this by first showing that these assumptions entail
.
We can do this by first showing that these assumptions entail 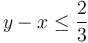 , and then showing that
, and then showing that 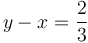 is consistent with the assumptions.
is consistent with the assumptions.
We use the same basic skeleton of includes/namespaces/main as before. We make an ExprManager and SmtEngine as before.
ExprManager em; SmtEngine smt(&em);
We now set on option on the SmtEngine to enable incremental or multiple query solving, which we will take advantage of.
smt.setOption("incremental", SExpr("true")); // Enable incremental solving
We get the Types real and integer from em, and we make x and y variables of the respective types.
Type real = em.realType();
Type integer = em.integerType();
Expr x = em.mkVar("x", integer);
Expr y = em.mkVar("y", real);
We now make Exprs for the 3 Rational constants in the formulas using em.mkConst():
Expr three = em.mkConst(Rational(3)); Expr neg2 = em.mkConst(Rational(-2)); Expr two_thirds = em.mkConst(Rational(2,3));
We will now make the intermediate terms using mkExpr.
Expr three_y = em.mkExpr(kind::MULT, three, y); Expr diff = em.mkExpr(kind::MINUS, y, x);
The first argument to mkExpr is a Kind. Kind is an enum covering all of the various expressions that CVC4 can make. Common operators have fairly standard ALL_CAPS names, such as LEQ, MINUS, AND, BITVECTOR_NAND, and so on. Kind's are in the namespace CVC4::kind. For more information see Expr#Constants.
Using these intermediate terms, we make the following formulas in the same way we made terms.
Expr x_geq_3y = em.mkExpr(kind::GEQ, x, three_y); Expr x_leq_y = em.mkExpr(kind::LEQ, x, y); Expr neg2_lt_x = em.mkExpr(kind::LT, neg2, x);
We now assert the assumptions in the SmtEngine:
Expr assumptions = em.mkExpr(kind::AND, x_geq_3y, x_leq_y, neg2_lt_x); smt.assertFormula(assumptions);
Alternatively, we could have asserted x_geq_3y, x_leq_y, and neg2_lt_x individually. It is worth pointing out that these are asserted at decision level 0. Modern DPLL(T) solvers are stack based. We can push the stack(), add assertions and then pop() assertions off of the stack.
We can now prove that 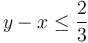 . We first make an Expr for this literal. We now push() the SmtEngine, query the SmtEngine for the validity of the literal given the assumptions, and pop() the SmtEngine.
. We first make an Expr for this literal. We now push() the SmtEngine, query the SmtEngine for the validity of the literal given the assumptions, and pop() the SmtEngine.
smt.push(); Expr diff_leq_two_thirds = em.mkExpr(kind::LEQ, diff, two_thirds); cout << "Prove that " << diff_leq_two_thirds << " with CVC4." << endl; cout << "CVC4 should report VALID." << endl; cout << "Result from CVC4 is: " << smt.query(diff_leq_two_thirds) << endl; smt.pop();
It is worth noting that the push() and pop() are not strictly needed in order to not effect context level 0. This is because SmtEngine guards query(phi), checkSat(phi) with internal pushes and pops so phi does not effect the current context. It is needed below; however, as the second lemma is proved in the following fashion:
smt.push(); Expr diff_is_two_thirds = em.mkExpr(kind::EQUAL, diff, two_thirds); smt.assertFormula(diff_is_two_thirds); cout << "Show that the asserts are consistent with " << endl; cout << diff_is_two_thirds << " with CVC4." << endl; cout << "CVC4 should report SAT." << endl; cout << "Result from CVC4 is: " << smt.checkSat(em.mkConst(true)) << endl; smt.pop();
bitvectors
In this example we will prove the equivalence of three different pieces of code. The example is adapted from the book A Hacker's Delight by Henry S. Warren. The code can be found in /examples/api/bitvectors.cpp. Given a variable x, that can only have one of two values: a or b, we want to assign to x a value different than the current one. For example if x was equal to a we want to assign to it b. The most straightforward implementation of this is the following:
if (x == a) x = b; else x = a;
or more concise:
x = x == a ? b : a; // (0)
However, the following two pieces of code provide a more efficient implementation:
x = a + b - x; // (1)
or
x = a ^ b ^ x; // (2)
We will encode the problem using the theory of bit-vectors and check that the three implementations are indeed equivalent. Let's analyze the code in bitvector.cpp line by line. Because we are interested in checking two different problems we will turn on incremental mode and specify the logic, to increase efficiency of solving:
smt.setOption("incremental", true); // Enable incremental solving
smt.setLogic("QF_BV"); // Set the logic
To make a bit-vector variable we must first make a bit-vector type. The factory method that constructs a bit-vector type requires the width of the bit-vector as an argument. In our example we will assume we are modeling a 32-bit machine:
// Creating a bit-vector type of width 32 Type bitvector32 = em.mkBitVectorType(32);
Creating variables and expressions follows the same pattern as in previous examples. We will first create the input variables x, a and b:
// Variables
Expr x = em.mkVar("x", bitvector32);
Expr a = em.mkVar("a", bitvector32);
Expr b = em.mkVar("b", bitvector32);
The first assumption constraints x to be equal to either a or b:
// First encode the assumption that x must be equal to a or b Expr x_eq_a = em.mkExpr(kind::EQUAL, x, a); Expr x_eq_b = em.mkExpr(kind::EQUAL, x, b); Expr assumption = em.mkExpr(kind::OR, x_eq_a, x_eq_b);
Because we will need this assumption to prove all following properties we can just assert it to the solver in the current context.
// Assert the assumption smt.assertFormula(assumption);
To model the semantics of the instructions we need to introduce a new variable for x for each program state. Here new_x will represent the value of x after executing code (0). We will use new_x_ to represent the value of x after executing code (1) first, and then after executing code (2).
// Introduce a new variable for the new value of x after assignment.
Expr new_x = em.mkVar("new_x", bitvector32); // x after executing code (0)
Expr new_x_ = em.mkVar("new_x_", bitvector32); // x after executing code (1) or (2)
We can encode the assignment in code (0) in a straightforward manner by using a term-ITE (if-then-else) expression which captures the semantics of the C++ (cond ? val1 : val2).
// new_x = x == a ? b : a; Expr ite = em.mkExpr(kind::ITE, x_eq_a, b, a); Expr assignment0 = em.mkExpr(kind::EQUAL, new_x, ite);
// Assert the encoding of code (0) cout << "Asserting " << assignment0 << " to CVC4 " << endl; smt.assertFormula(assignment0);
Because the assertions we have so far are the only ones that will be used in both queries we can now push a new context:
cout << "Pushing a new context." << endl; smt.push();
Next, we move to encoding the semantics of code (1) in a similar manner as before:
// Encoding code (1) // new_x_ = a xor b xor x Expr a_xor_b_xor_x = em.mkExpr(kind::BITVECTOR_XOR, a, b, x); Expr assignment1 = em.mkExpr(kind::EQUAL, new_x_, a_xor_b_xor_x);
// Assert encoding to CVC4 in current context; cout << "Asserting " << assignment1 << " to CVC4 " << endl; smt.assertFormula(assignment1);
And we check that the value of x after executing code (0) is the same as that after executing code (1):
Expr new_x_eq_new_x_ = em.mkExpr(kind::EQUAL, new_x, new_x_); cout << " Querying: " << new_x_eq_new_x_ << endl; cout << " Expect valid. " << endl; cout << " CVC4: " << smt.query(new_x_eq_new_x_) << endl;
Note that we are using smt.query(f) which checks for the validity of the formula f under the current assumptions i.e. that checking whether the current assertions imply (not f) is unsat. Now that we are done with checking the first equivalence, we can pop the context:
cout << " Popping context. " << endl; smt.pop();
Note that poping the context will remove the assertion saying new_x_ = a xor b xor x.
We follow a similar pattern to check the second equivalence:
// Encoding code (2) // new_x_ = a + b - x Expr a_plus_b = em.mkExpr(kind::BITVECTOR_PLUS, a, b); Expr a_plus_b_minus_x = em.mkExpr(kind::BITVECTOR_SUB, a_plus_b, x); Expr assignment2 = em.mkExpr(kind::EQUAL, new_x_, a_plus_b_minus_x); // Assert encoding to CVC4 in current context; cout << "Asserting " << assignment2 << " to CVC4 " << endl; smt.assertFormula(assignment2);
cout << " Querying: " << new_x_eq_new_x_ << endl; cout << " Expect valid. " << endl; cout << " CVC4: " << smt.query(new_x_eq_new_x_) << endl;
Here is another example (extract.cpp) that demonstrates how to use the extract operator:
ExprManager em;
SmtEngine smt(&em);
smt.setLogic("QF_BV"); // Set the logic
Type bitvector32 = em.mkBitVectorType(32);
Expr x = em.mkVar("a", bitvector32);
Expr ext_31_1 = em.mkConst(CVC4::BitVectorExtract(31,1));
Expr x_31_1 = em.mkExpr(ext_31_1, x);
Expr ext_30_0 = em.mkConst(CVC4::BitVectorExtract(30,0));
Expr x_30_0 = em.mkExpr(ext_30_0, x);
Expr ext_31_31 = em.mkConst(CVC4::BitVectorExtract(31,31));
Expr x_31_31 = em.mkExpr(ext_31_31, x);
Expr ext_0_0 = em.mkConst(CVC4::BitVectorExtract(0,0));
Expr x_0_0 = em.mkExpr(ext_0_0, x);
Expr eq = em.mkExpr(kind::EQUAL, x_31_1, x_30_0);
cout << " Asserting: " << eq << endl;
smt.assertFormula(eq);
Expr eq2 = em.mkExpr(kind::EQUAL, x_31_31, x_0_0);
cout << " Querying: " << eq2 << endl;
cout << " Expect valid. " << endl;
cout << " CVC4: " << smt.query(eq2) << endl;
Sets
If setting the logic, use "FS" to enable theory of sets.
smt.setLogic("QF_UFLIAFS");
To create a set type, call mkSetType in the ExprManager. It takes as argument the element type.
Type integer = em.integerType(); Type set = em.mkSetType(integer);
Union and Intersection
Verify union distributions over intersection. Checks the validity of (A union B) intersection C = (A intersection C) union (B intersection C) for all sets A, B, C of integers.
Expr A = em.mkVar("A", set);
Expr B = em.mkVar("B", set);
Expr C = em.mkVar("C", set);
Expr unionAB = em.mkExpr(kind::UNION, A, B);
Expr lhs = em.mkExpr(kind::INTERSECTION, unionAB, C);
Expr intersectionAC = em.mkExpr(kind::INTERSECTION, A, C);
Expr intersectionBC = em.mkExpr(kind::INTERSECTION, B, C);
Expr rhs = em.mkExpr(kind::UNION, intersectionAC, intersectionBC);
Expr theorem = em.mkExpr(kind::EQUAL, lhs, rhs);
cout << "CVC4 reports: " << theorem << " is " << smt.query(theorem) << "." << endl;
EmptySet constant and Subset predicate
An object of CVC4::EmptySet carries its type, which should be given at construction time. Note that this is the type of the set itself (so, pass the type set of integers, not integers).
Then, the empty set constant can be define using mkConst passing this CVC4::EmptySet object.
Expr A = em.mkVar("A", set);
Expr emptyset = em.mkConst(EmptySet(set));
Expr theorem = em.mkExpr(kind::SUBSET, emptyset, A);
cout << "CVC4 reports: " << theorem << " is " << smt.query(theorem) << "." << endl;
Membership, singleton and producing models
Remember to enable models (this should be done at the start, just after creating the smt engine).
smt.setOption("produce-models", true);
Find an element in {1, 2} intersection {2, 3}, if there is one.
// Integer constants
Expr one = em.mkConst(Rational(1));
Expr two = em.mkConst(Rational(2));
Expr three = em.mkConst(Rational(3));
// Singleton sets for each of these constants
Expr singleton_one = em.mkExpr(kind::SINGLETON, one);
Expr singleton_two = em.mkExpr(kind::SINGLETON, two);
Expr singleton_three = em.mkExpr(kind::SINGLETON, three);
// Build bigger sets using union
Expr one_two = em.mkExpr(kind::UNION, singleton_one, singleton_two);
Expr two_three = em.mkExpr(kind::UNION, singleton_two, singleton_three);
Expr intersection = em.mkExpr(kind::INTERSECTION, one_two, two_three);
Expr x = em.mkVar("x", integer);
Expr e = em.mkExpr(kind::MEMBER, x, intersection);
Result result = smt.checkSat(e);
cout << "CVC4 reports: " << e << " is " << result << "." << endl;
// If the formula was satisfiable (which it should be here), get the value of x.
if(result == Result::SAT) {
cout << "For instance, " << smt.getValue(x) << " is a member." << endl;
}
Strings
The example can be found in examples/api/strings.cpp
If setting the logic, use "S" to enable theory of strings.
smt.setLogic("S");
To create a string type, call mkSetType in the ExprManager.
Type string = em.stringType();
Make some string literals:
// std::string
std::string std_str_ab("ab");
// CVC4::String
CVC4::String cvc4_str_ab(std_str_ab);
CVC4::String cvc4_str_abc("abc");
// String constants
Expr ab = em.mkConst(cvc4_str_ab);
Expr abc = em.mkConst(CVC4::String("abc"));
Make some string variables:
Expr x = em.mkVar("x", string);
Expr y = em.mkVar("y", string);
Expr z = em.mkVar("z", string);
Make some string constraints:
// String concatenation: x.ab.y
Expr lhs = em.mkExpr(kind::STRING_CONCAT, x, ab, y);
// String concatenation: abc.z
Expr rhs = em.mkExpr(kind::STRING_CONCAT, abc, z);
// x.ab.y = abc.z
Expr formula1 = em.mkExpr(kind::EQUAL, lhs, rhs);
// Length of y: |y|
Expr leny = em.mkExpr(kind::STRING_LENGTH, y);
// |y| >= 0
Expr formula2 = em.mkExpr(kind::GEQ, leny, em.mkConst(Rational(0)));
// Regular expression: (ab[c-e]*f)|g|h
Expr r = em.mkExpr(kind::REGEXP_UNION,
em.mkExpr(kind::REGEXP_CONCAT,
em.mkExpr(kind::STRING_TO_REGEXP, em.mkConst(String("ab"))),
em.mkExpr(kind::REGEXP_STAR,
em.mkExpr(kind::REGEXP_RANGE, em.mkConst(String("c")), em.mkConst(String("e")))),
em.mkExpr(kind::STRING_TO_REGEXP, em.mkConst(String("f")))),
em.mkExpr(kind::STRING_TO_REGEXP, em.mkConst(String("g"))),
em.mkExpr(kind::STRING_TO_REGEXP, em.mkConst(String("h"))));
// String variables
Expr s1 = em.mkVar("s1", string);
Expr s2 = em.mkVar("s2", string);
// String concatenation: s1.s2
Expr s = em.mkExpr(kind::STRING_CONCAT, s1, s2);
// s1.s2 in (ab[c-e]*f)|g|h
Expr formula3 = em.mkExpr(kind::STRING_IN_REGEXP, s, r);
Make a query:
Expr q = em.mkExpr(kind::AND, formula1, formula2, formula3);
Check the result:
Result result = smt.checkSat(q);
std::cout << "CVC4 reports: " << q << " is " << result << "." << std::endl;
if(result == Result::SAT) {
std::cout << " x = " << smt.getValue(x) << std::endl;
std::cout << " s1.s2 = " << smt.getValue(s) << std::endl;
}
Java API
Parallel Solving
Obtaining
- Download a statically built binary supporting parallel solving: Optimized build
- If compiling from source, specify by --with-portfolio option to the configure script. This will create an additional binary pcvc4 which supports parallel solving.
./configure --with-portfolio [...]
Running
- The pcvc4 binary allows the user to run multiple instances of the solver simultaneously on the input problem. Each thread can be configured differently by prefixing each thread-specific options by --threadN=<thread-specific-option> where N is the thread number (counting from 0). For example,
pcvc4 --thread0=--decision=internal --thread0=--no-simplification --thread1=--decision=justification input.smt2
will run two solver threads with different decision heuristics and simplification switched off for thread0. The solver will stop as soon as one of threads has an answer.
- The default number of threads is 2. The number of threads can be specified using --threads option. Note that any of the options specified outside all of the --threadi=... will be applied to all threads. For instance, in
pcvc4 --threads=3 \
--thread0=--random-seed=10 \
--thread1=--random-seed=20 \
--thread2=--random-seed=30 \
--simplification=none \
input.smt2
three threads will be run, all with simplification disabled, and different random seeds for the SAT solver.
- We also allow sharing of conflict clauses across different threads. By default, this is disabled but may he enabled by using the --filter-lemma-length option. For example,
pcvc4 --filter-lemma-length=5 ...
will share all lemmas having 5 or fewer literals.
