Difference between revisions of "Separation Logic"
| Line 28: | Line 28: | ||
| <math>I,h \models_{SL} </math> (sep <math>\phi_1 \ldots \phi_n</math>) | | <math>I,h \models_{SL} </math> (sep <math>\phi_1 \ldots \phi_n</math>) | ||
| Iff | | Iff | ||
| − | | there exist heaps <math>h_1, | + | | there exist heaps <math>h_1,\ldots,h_n</math> s.t. <math>h=h_1\uplus \ldots \uplus h_2</math> and <math>I,h_i \models_{SL} \phi_i, i = 1,\ldots,n</math> |
|- | |- | ||
| − | | <math>I,h \models_{SL} \phi_1 | + | | <math>I,h \models_{SL}</math> (wand <math>\phi_1 \phi_2</math>) |
| Iff | | Iff | ||
| for all heaps <math>h'</math> if <math>h'\#h</math> and <math>I,h' \models_{SL} \phi_1</math> then <math>I,h'\uplus h \models_{SL} \phi_2</math> | | for all heaps <math>h'</math> if <math>h'\#h</math> and <math>I,h' \models_{SL} \phi_1</math> then <math>I,h'\uplus h \models_{SL} \phi_2</math> | ||
Revision as of 12:22, 28 November 2016
CVC4 supports a syntax for separation logic as an extension of the *.smt2 language.
Signature and semantics
Given a base theory T, CVC4 supports reasoning about SL(T)_{Loc,Data} formulas, where "Loc" and "Data" are any sort belonging to T. A SL(T)_{Loc,Data} formula is one from the following grammar:
F : L | (emp t1 t2) | (pto t1 t2) | (sep F1 ... Fn) | (wand F1 F2) | ~F1 | F1 op ... op Fn
where "op" is any classical Boolean connective, t1 and t2 are terms in the signature of T of sort Loc and Data respectively, and L is a T-literal. The operator "emp" denotes the empty heap constraint, the operator "pto" denotes the points-to predicate, the operator "sep" denotes separation start and is variadic, and the operator "wand" denote magic wand.
The semantics of these operators are as follows:
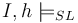 L L
|
Iff | 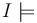 L, if L is a L, if L is a 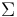 -formula -formula
|
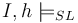 (emp t u) (emp t u)
|
Iff | h = \emptyset |
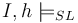 (pto t u) (pto t u)
|
Iff | 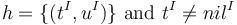
|
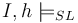 (sep (sep  ) )
|
Iff | there exist heaps  s.t. s.t. 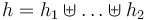 and and 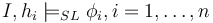
|
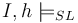 (wand (wand 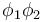 ) )
|
Iff | for all heaps 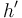 if if 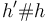 and and 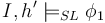 then then 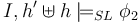
|
Notice that the arguments of "emp" are used to denote the type of the heap and have no meaning otherwise.
The sorts Loc and Data are inferred by CVC4, and must be consistent across all predicates occurring in an input. CVC4 does not accept an input such as:
(declare-sort U 0) (declare-const x U) (assert (and (pto x 0) (pto 1 2)))
since the sorts of the first arguments of the points-to predicates do not agree.
Syntax
Separation logic in CVC4 requires the "all supported" logic:
(set-logic QF_ALL_SUPPORTED)
The syntax for the operators of separation logic is summarized in the following table:
| CVC language | SMTLIB language | C++ API | |
|---|---|---|---|
| Empty heap | N/A
|
(emp X Y)
|
em.mkExpr(kind::SEP_EMP, X, Y);
|
| Points-to | N/A
|
(pto X Y)
|
em.mkExpr(kind::SEP_PTO, X, Y);
|
| Separation star | N/A
|
(sep C1 ... Cn)
|
em.mkExpr(kind::SEP_STAR, C1, ..., Cn);
|
| Magic wand | N/A
|
(wand C1 C2)
|
em.mkExpr(kind::SEP_WAND, C1, C2);
|
| Nil element | N/A
|
(as nil T)
|
em.mkUniqueVar(T,kind::SEP_NIL);
|
Examples
The following input on heaps Int -> Int is unsatisfiable:
(set-logic QF_ALL_SUPPORTED) (set-info :status unsat) (declare-const x Int) (declare-const a Int) (declare-const b Int) (assert (and (pto x a) (pto x b))) (assert (not (= a b))) (check-sat)
The following input on heaps Int -> Node is satisfiable, where Node denotes a user-defined inductive datatype:
(set-logic QF_ALL_SUPPORTED) (set-info :status sat) (declare-const x Int) (declare-const y Int) (declare-const z Int) (declare-datatypes () ((Node (node (data Int) (left Int) (right Int))))) (assert (pto x (node 0 y z))) (check-sat)
