User Manual
This manual includes lots of information about how to use CVC4.
It is a work in-progress.
Contents
- 1 What is CVC4?
- 2 Obtaining and compiling CVC4
- 2.1 Obtaining binary packages
- 2.2 Obtaining source packages
- 2.3 Source repository
- 2.4 Building from source
- 2.4.1 Quick-start instructions
- 2.4.2 Common make Options
- 2.4.3 Common configure Options
- 2.4.4 Build dependencies
- 2.4.5 Optional requirements
- 2.4.6 Language bindings
- 2.4.7 Building CVC4 from a repository checkout
- 2.4.8 Examples and tutorials are not built or installed
- 2.4.9 Appendix: Build architecture
- 3 Using the CVC4 binary
- 4 CVC4's native input language
- 5 CVC4's support for the SMT-LIB language
- 6 The CVC4 library interface (API)
- 7 Upgrading from CVC3 to CVC4
- 8 Useful command-line options
- 9 Dumping API calls or preprocessed output
- 10 Changing the output language
- 11 Proof support
- 12 Portfolio solving
- 13 Emacs support
What is CVC4?
CVC4 is the last of a long line of SMT solvers that started with SVC and includes CVC, CVC-Lite and CVC3. Technically, it is an automated validity checker for a many-sorted (i.e., typed) first-order logic with built-in theories. The current built-in theories are the theories of:
- equality over free (aka uninterpreted) function and predicate symbols,
- real and integer linear arithmetic (with some support for non-linear arithmetic),
- bit vectors,
- arrays,
- tuples,
- records,
- user-defined inductive data types.
CVC4 checks whether a given formula 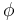 is valid in the built-in theories under a given set
is valid in the built-in theories under a given set 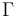 of assumptions, a context.
More precisely, it checks whether
of assumptions, a context.
More precisely, it checks whether
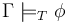
that is, whether 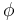 is a logical consequence in
is a logical consequence in 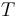 of the set of formulas
of the set of formulas 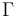 , where
, where 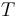 is the union of CVC4's built-in theories.
is the union of CVC4's built-in theories.
Roughly speaking, when 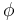 is a universal formula and
is a universal formula and 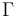 is a set of existential formulas (i.e., when
is a set of existential formulas (i.e., when 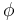 and
and 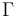 contain at most universal, respectively existential, quantifiers), CVC4 is a decision procedure:
it is guaranteed (modulo bugs and memory limits) to return a correct "valid" or "invalid" answer eventually.
In all other cases, CVC4 is deductively sound but incomplete:
it will never say that an invalid formula is valid,
but it may either never return or give up and return "unknown" for some formulas.
contain at most universal, respectively existential, quantifiers), CVC4 is a decision procedure:
it is guaranteed (modulo bugs and memory limits) to return a correct "valid" or "invalid" answer eventually.
In all other cases, CVC4 is deductively sound but incomplete:
it will never say that an invalid formula is valid,
but it may either never return or give up and return "unknown" for some formulas.
Currently, when CVC4 returns "valid" for a query formula 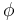 under a context
under a context 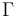 it provides no evidence to back its claim.
Future versions will also return a proof certificate,
a formal proof that
it provides no evidence to back its claim.
Future versions will also return a proof certificate,
a formal proof that 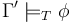 for some subset
for some subset 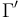 of
of 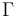 .
.
When CVC4 returns "invalid" it can return
both a counter-example to 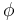 's validity under the context
's validity under the context 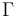 and a counter-model.
Both a counter-example and a counter-model are a set
and a counter-model.
Both a counter-example and a counter-model are a set  of additional formulas consistent with
of additional formulas consistent with 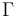 in
in 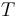 , but entailing the negation of
, but entailing the negation of 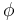 .
Formally:
.
Formally:
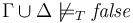 and
and
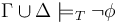 .
.
The difference is that a counter-model is given as a set of equations providing a concrete assignment of values for the free symbols in 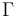 and
and 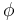 (see the section on CVC4's native input language for more details).
(see the section on CVC4's native input language for more details).
Obtaining and compiling CVC4
CVC4 is distributed in the following ways:
Obtaining binary packages
Binary packages are available for CVC4. Nightly builds:
Obtaining source packages
Sources are available from the same site as the binaries.
Source repository
The CVC4 source repository is currently hosted by CIMS and requires a CIMS account. Please contact a member of the development team for access. Please see the additional instructions for #Building_CVC4 from_a_repository_checkout here.
Building from source
Quick-start instructions
To compile from a source package:
- Install antlr
- Configure cvc4
- Compile cvc4
- Install cvc4 [optional]
cd contrib ./get-antlr-3.4 cd .. ./configure --with-antlr-dir=`pwd`/antlr-3.4 ANTLR=`pwd`/antlr-3.4/bin/antlr3 make make check [recommended] make install [optional]
(To build from a repository checkout, see below.)
Common make Options
- "make install" will install into the "--prefix" option you gave to
the configure script (/usr/local by default).
./configure --prefix=~/install_targets/cvc4 ... make install
- You should run "make check" before installation to ensure that CVC4 has been
built correctly. In particular, GCC version 4.5.1 seems to have a bug in the optimizer that results in incorrect behavior (and wrong results) in many builds. This is a known problem for Minisat, and since Minisat is at the core of CVC4, a problem for CVC4. "make check" easily detects this problem (by showing a number of FAILed test cases). It is ok if the unit tests aren't run as part of "make check", but all system tests and regression tests should pass without incident.
- To build API documentation, use "make doc". Documentation is produced
under builds/doc/ but is not installed by "make install".
Examples and tutorials are not installed with "make install." See below.
For more information about the build system itself (probably not necessary for casual users), see the Appendix at the bottom of this file.
Common configure Options
- --prefix=PREFIX install architecture-independent files in PREFIX (by default /usr/local)
- --with-build={production,debug,default,competition}
- --with-antlr-dir=PATH
- --with-cln/--with-gmp selects the numbers package to use by default (#Optional requirements)
- --enable-static-binary build a fully statically-linked binary. (This is recommended for Mac OS X users that want to be able to use gdb.)
- ANTLR=PATH location of the antlr3 script
- --with-boost=DIR installation location of the boost libraries (most users will not need this)
See ./configure --help for more.
Build dependencies
The following tools and libraries are required to run CVC4. Versions given are minimum versions; more recent versions should be compatible.
- GNU C and C++ (gcc and g++), reasonably recent versions
- GNU Make
- GNU Bash
- GMP v4.2 (GNU Multi-Precision arithmetic library)
- libantlr3c v3.2 or v3.4 (ANTLR parser generator C support library)
- The Boost C++ base libraries
- MacPorts [highly recommended if on a Mac; see #MacPorts]
The hardest to obtain and install is the libantlr3c requirement, and
is explained next.
If "make" is non-GNU on your system, make sure to invoke "gmake" (or whatever GNU Make is installed as). If your usual shell is not Bash, the configure script should auto-correct this. If it does not, you'll see strange shell syntax errors, and you may need to explicitly set SHELL or CONFIG_SHELL to the location of bash on your system.
Installing libantlr3c: ANTLR parser generator C support library
For libantlr3c, you can use the convenience script in contrib/get-antlr-3.4 in the source distribution---this will download, patch, compile and install libantlr3c into your cvc4 directory as cvc4/antlr-3.4/.
cd contrib ./get-antlr-3.4
CVC4 must be configured with the antlr library installation directory, --with-antlr-dir, and an antlr executable script file, ANTLR. If libantlr3c was installed via get-antlr-3.4, the following configure line should suffice for CVC44
./configure --with-antlr-dir=`pwd`/antlr-3.4 ANTLR=`pwd`/antlr-3.4/bin/antlr3
For 64 bit machines, libantlr3c needs to be configured with 64 bit explicitly
./configure --enable-64bit ...
The get-antlr-3.4 script makes a guess at whether the machine is 64 bit and adds the appropriate flag. To force the script to compile 32 bit:
MACHINE_TYPE="x86" ./get-antlr3.4
To force the script to compile 64 bit:
MACHINE_TYPE="x86_64" ./get-antlr3.4
For a longer discussion, instructions for manual installation, and more in depth troubleshooting, see Developer's Guide#ANTLR3.
MacPorts
On a Mac, it is highly recommended that you use MacPorts (see http://www.macports.org/). Doing so is easy. Then, simply run the script contrib/mac-build, which installs a few ports from the MacPorts repository, then compiles and installs antlr3c using the get-antlr-3.4 script. The mac-build script should set you up with all requirements, and will tell you how to configure CVC4 when it completes successfully.
Installing the Boost C++ base libraries
A Boost package is available on most Linux distributions; check yours for a package named something like libboost-dev or boost-devel. There are a number of additional Boost packages in some distributions, but this "basic" one should be sufficient for building CVC4.
Should you want to install Boost manually, or to learn more about the Boost project, please visit http://www.boost.org/.
Optional requirements
None of these is required, but can improve CVC4 as described below:
- Optional: SWIG 2.0.x (Simplified Wrapper and Interface Generator)
- Optional: CLN v1.3 or newer (Class Library for Numbers)
- Optional: CUDD v2.4.2 or newer (Colorado University Decision Diagram package)
- Optional: GNU Readline library (for an improved interactive experience)
- Optional: The Boost C++ threading library (libboost_thread)
- Optional: CxxTest unit testing framework
SWIG is necessary to build the Java API (and of course a JDK is necessary, too). SWIG 1.x won't work; you'll need 2.0, and the more recent the better. On Mac, we've seen SWIG segfault when generating CVC4 language bindings; version 2.0.8 or higher is recommended to avoid this. See Language bindings below for build instructions.
CLN is an alternative multiprecision arithmetic package that can offer better performance and memory footprint than GMP. CLN is covered by the GNU General Public License, version 3; so if you choose to use CVC4 with CLN support, you are licensing CVC4 under that same license. (Usually CVC4's license is more permissive than GPL is; see the file COPYING in the CVC4 source distribution for details.) Please visit http://www.ginac.de/CLN/ for more details about CLN.
CUDD is a decision diagram package that changes the behavior of the CVC4 arithmetic solver in some cases; it may or may not improve the arithmetic solver's performance. See below for instructions on obtaining and building CUDD.
The GNU Readline library is optionally used to provide command editing, tab completion, and history functionality at the CVC prompt (when running in interactive mode). Check your distribution for a package named "libreadline-dev" or "readline-devel" or similar.
The Boost C++ threading library (often packaged independently of the Boost base library) is needed to run CVC4 in "portfolio" (multithreaded) mode. Check your distribution for a package named "libboost-thread-dev" or similar.
CxxTest is necessary to run CVC4's unit tests (included with the distribution). Running these is not really required for users of CVC4; "make check" will skip unit tests if CxxTest isn't available, and go on to run the extensive system- and regression-tests in the source tree. However, if you're interested, you can download CxxTest at http://cxxtest.com/ .
Building with CUDD (optional)
CUDD, if desired, must be installed delicately. The CVC4 configure script attempts to auto-detect the locations and names of CUDD headers and libraries the way that the Fedora RPMs install them, the way that our NYU-provided Debian packages install them, and the way they exist when you download and build the CUDD sources directly. If you install from Fedora RPMs or our Debian packages, the process should be completely automatic, since the libraries and headers are installed in a standard location. If you download the sources yourself, you need to build them in a special way. Fortunately, the "contrib/build-cudd-2.4.2-with-libtool.sh" script in the CVC4 source tree does exactly what you need: it patches the CUDD makefiles to use libtool, builds the libtool libraries, then reverses the patch to leave the makefiles as they were. Once you run this script on an unpacked CUDD 2.4.2 source distribution, then CVC4's configure script should pick up the libraries if you provide --with-cudd-dir=/PATH/TO/CUDD/SOURCES.
If you want to force linking to CUDD, provide --with-cudd to the configure script; this makes it a hard requirement rather than an optional add-on.
The NYU-provided Debian packaging of CUDD 2.4.2 and CUDD 2.5.0 are here (along with the CVC4 Debian packages):
deb http://cvc4.cs.nyu.edu/debian/ unstable/
On Debian (and Debian-derived distributions like Ubuntu), you only need to drop that one line in your /etc/apt/sources.list file, then install with your favorite package manager.
The Debian source package "cudd", available from the same repository, includes a diff of all changes made to cudd makefiles.
Language bindings
There are several options available for using CVC4 from the API.
First, CVC4 offers a complete and flexible API for manipulating expressions, maintaining a stack of assertions, and checking satisfiability, and related things. The C++ libraries (libcvc4.so and libcvc4parser.so) and required headers are installed normally via a "make install". This API is also available from Java (via CVC4.jar and libcvc4jni.so) by configuring with --enable-language-bindings=java. You'll also need SWIG 2.0 installed (and you might need to help configure find it if you installed it in a nonstandard place with --with-swig-dir=/path/to/swig/installation). You may also need to give the configure script the path to your Java headers (in particular, jni.h). You might do so with (for example):
./configure --enable-language-bindings=java \
JAVA_CPPFLAGS=-I/usr/lib/jvm/java-6-openjdk-amd64/include
There is also a "C++ compatibility API" (#include <cvc4/cvc3_compat.h> and link against libcvc4compat.so) that attempts to maintain source-level backwards-compatibility with the CVC3 C++ API. The compatibility library is built by default, and --enable-language-bindings=java enables the Java compatibility library (CVC4compat.jar and libcvc4compatjni.so). --enable-language-bindings=c enables the C compatibility library (#include <cvc4/bindings/compat/c/c_interface.h> and link against libcvc4bindings_c_compat.so), and if you want both C and Java bindings, use --enable-language-bindings=c,java. These compatibility language bindings do NOT require SWIG.
The examples/ directory in the source distribution includes some basic examples (the "simple vc" and "simple vc compat" family of examples) of all these interfaces.
In principle, since we use SWIG to generate the native Java API, we could support other languages as well. However, using CVC4 from other languages is not supported, nor expected to work, at this time. If you're interested in helping to develop, maintain, and test a language binding, please contact us via the users' mailing list at cvc-users@cs.nyu.edu.
Building CVC4 from a repository checkout
The following tools and libraries are additionally required to build CVC4 from from a repository checkout rather than from a prepared source tarball.
- Automake v1.11
- Autoconf v2.61
- Libtool v2.2
- ANTLR3 v3.2 or v3.4
- Java Development Kit (required for ANTLR3)
First, use "./autogen.sh" to create the configure script. Then proceed as normal for any distribution tarball. The parsers are pre-generated for the tarballs, but don't exist in the repository; hence the extra ANTLR3 and JDK requirements to generate the source code for the parsers, when building from the repository.
Examples and tutorials are not built or installed
Examples are not built by "make" or "make install". See examples/README in the source distribution for information on what to find in the examples/ directory, as well as information about building and installing them.
Appendix: Build architecture
The build system is generated by automake, libtool, and autoconf. It is somewhat nonstandard, though, which (for one thing) requires that GNU Make be used. If you ./configure in the top-level source directory, the objects will actually all appear in builds/${arch}/${build_id}. This is to allow multiple, separate builds in the same place (e.g., an assertions-enabled debugging build alongside a production build), without changing directories at the shell. The "current" build is maintained, and you can still use (e.g.) "make -C src/main" to rebuild objects in just one subdirectory.
You can also create your own build directory inside or outside of the source tree and configure from there. All objects will then be built in that directory, and you'll ultimately find the "cvc4" binary in src/main/, and the libraries under src/ and src/parser/.
Using the CVC4 binary
The CVC4 driver binary ("cvc4"), once installed, can be executed directly to enter into interactive mode:
$ cvc4 cvc4 1.0 assertions:off CVC4>
You can then enter commands into CVC4 interactively:
CVC4> OPTION "incremental"; CVC4> OPTION "produce-models"; CVC4> TRANSFORM 25*25; 625 CVC4> x, y : INT; CVC4> QUERY x = y; invalid CVC4> COUNTERMODEL; x : INT = -1; y : INT = 0; CVC4> ASSERT x >= 0; CVC4> QUERY x = y; invalid CVC4> COUNTERMODEL; x : INT = 0; y : INT = 1; CVC4>
The above example shows two useful options, incremental and produce-models.
- The incremental option allows you to issue multiple QUERY (or CHECKSAT) commands, and allows the use of the PUSH and POP commands. Without this option, CVC4 optimizes itself for a single QUERY or CHECKSAT command (though you may issue any number of ASSERT commands). The incremental option may also be given by passing the -i command line option to CVC4.
- The produce-models option allows you to query the model (here, with the COUNTERMODEL command) after an "invalid" QUERY (or "satisfiable" CHECK-SAT). Without it, CVC4 doesn't do the bookkeeping necessary to support model generation. The produce-models option may also be given by passing the -m command line option to CVC4.
So, if you invoke CVC4 with -im, you don't need to pass those options at all:
$ cvc4 -im cvc4 1.0 assertions:off CVC4> x, y : INT; CVC4> QUERY x = y; invalid CVC4> COUNTERMODEL; x : INT = -1; y : INT = 0; CVC4> ASSERT x >= 0; CVC4> QUERY x = y; invalid CVC4> COUNTERMODEL; x : INT = 0; y : INT = 1; CVC4>
By default, CVC4 operates in CVC-language mode. If you enter something that looks like SMT-LIB, it will suggest that you use the "--lang smt" command-line option for SMT-LIB mode:
CVC4> (declare-fun x () Int) Parse Error: <shell>:1.7: In CVC4 presentation language mode, but SMT-LIB format detected. Use --lang smt for SMT-LIB support. CVC4>
Verbosity
CVC4 has various levels of verbosity. By default, CVC4 is pretty quiet, only reporting serious warnings and notices. If you're curious about what it's doing, you can pass CVC4 the -v option:
$ cvc4 -v file.smt2 Invoking: (set-logic AUFLIRA) Invoking: (set-info :smt-lib-version 2.000000) Invoking: (set-info :category "crafted") Invoking: (set-info :status unsat) Invoking: (declare-fun x () Real) etc...
For even more verbosity, you can pass CVC4 an additional -v:
$ cvc4 -vv file.smt2 Invoking: (set-logic AUFLIRA) Invoking: (set-info :smt-lib-version 2.000000) Invoking: (set-info :category "crafted") Invoking: (set-info :status unsat) Invoking: (declare-fun x () Real) etc... expanding definitions... constraining subtypes... applying substitutions... simplifying assertions... doing static learning... etc...
Internally, verbosity is just an integer value. It starts at 0, and with every -v on the command line it is incremented; with every -q, decremented. It can also be set directly. From CVC language:
CVC4> OPTION "verbosity" 2;
Or from SMT-LIB language:
CVC4> (set-option :verbosity 2)
Getting statistics
Statistics can be dumped on exit (both normal and abnormal exits) with the --statistics command line option.
$ cvc4 --statistics foo.smt2 sat sat::decisions, 0 sat::propagations, 3 sat::starts, 1 theory::uf::TheoryUF::functionTermsCount, 2 theory::uf::TheoryUF::mergesCount, 2 theory::uf::TheoryUF::termsCount, 6 theory<THEORY_UF>::propagations, 1 driver::filename, foo.smt2 driver::sat/unsat, sat driver::totalTime, 0.02015373 [many others]
Many statistics name-value pairs follow, one comma-separated pair per line.
Exit status
The exit status of CVC4 depends on the last QUERY or CHECK-SAT. If you wish to call CVC4 from a program (e.g., a shell script) and care only about the satisfiability or validity of a single formula, you can pass the -q option (as described above, under verbosity) and check the exit code. With -q, CVC4 should not produce any output unless it encounters a fatal error.
QUERY asks a validity question, and CHECK-SAT a satisfiability question, and these are dual problems; hence the terminology is different, but really "sat" and "invalid" are the same internally, as are "unsat" and "valid":
| Solver's last result | Exit code | Notes |
|---|---|---|
| sat or invalid | 10 | |
| unsat or valid | 20 | |
| unknown | 0 | could be for any reason: time limit exceeded, no memory, incompleteness.. |
| no result | 0 | no query or check-sat command issued |
| parse errors | 0 (in interactive mode) 1 (otherwise) | see below |
| other errors | 1 (usually) | see below |
Most "normal errors" return a 1 as the exit code, but out of memory conditions, and others, can produce different exit codes. In interactive mode, parse errors are ignored and the next line read; so in interactive mode, you may see an exit code of 0 even in the presence of such an error.
In SMT-LIB mode, an SMT-LIB command script that sets its status via "set-info :status" also affects the exit code. So, for instance, the following SMT-LIB script returns an exit code of 10 even though it contains no "check-sat" command:
(set-logic QF_UF) (set-info :status sat) (exit)
Without the "set-info," it would have returned an exit code of 0.
CVC4's native input language
The native input language consists of a sequence of symbol declarations and commands, each followed by a semicolon (;).
Any text after the first occurrence of a percent character and to the end of the current line is a comment:
%%% This is a native language comment
Type System
CVC4's type system includes a set of built-in types which can be expanded with additional user-defined types.
The type system consists of first-order types, subtypes of first-order types, and higher-order types, all of which are interpreted as sets. For convenience, we will sometimes identify below the interpretation of a type with the type itself.
First-order types consist of basic types and structured types. The basic types are 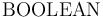 ,
, 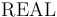 ,
, 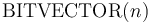 for all
for all 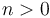 , as well as user-defined basic types (also called uninterpreted types).
The structured types are array, tuple, record types, and ML-style user-defined (inductive) datatypes.
, as well as user-defined basic types (also called uninterpreted types).
The structured types are array, tuple, record types, and ML-style user-defined (inductive) datatypes.
Note: Currently, subtypes consist only of the built-in subtype 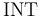 of
of 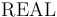 .
Support for CVC3-style user-defined subtypes will be added in a later release.
.
Support for CVC3-style user-defined subtypes will be added in a later release.
Function types are the only higher-order types. More precisely, they are just second-order types since function symbols in CVC4, both built-in and user-defined, can take as argument or return only values of a first-order type.
Basic Types
The BOOLEAN Type
The 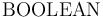 type is interpreted as the two-element set of Boolean values
type is interpreted as the two-element set of Boolean values
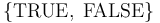 .
.
Note: CVC4's treatment of this type differs from CVC3's where 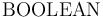 is used only as the type of formulas, but not as value type. CVC3 follows the two-tiered structure of classical first-order logic
which distinguishes between formulas and terms, and allows terms to occur in formulas but not vice versa (with the exception of the IF-THEN-ELSE construct).
CVC4 drops the distinction between terms and formulas and defines the latter just as terms of type
is used only as the type of formulas, but not as value type. CVC3 follows the two-tiered structure of classical first-order logic
which distinguishes between formulas and terms, and allows terms to occur in formulas but not vice versa (with the exception of the IF-THEN-ELSE construct).
CVC4 drops the distinction between terms and formulas and defines the latter just as terms of type 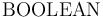 . As such, formulas can occur as subterms of possibly non-Boolean terms.
. As such, formulas can occur as subterms of possibly non-Boolean terms.
Example:
[To do]
The REAL Type
The 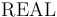 type is interpreted as the set of real numbers.
type is interpreted as the set of real numbers.
Note that these are the (infinite precision) mathematical reals, not the floating point numbers. Support for floating point types is planned for future versions.
x, y : REAL; QUERY (( x <= y ) AND ( y <= x )) => ( x = y );
The INT Type
The 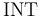 type is interpreted as the set of integer numbers
and is considered as a subtype of
type is interpreted as the set of integer numbers
and is considered as a subtype of 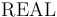 .
The latter means in particular that it is possible to mix integer and real terms
in expressions without the need of an explicit upcasting operator.
.
The latter means in particular that it is possible to mix integer and real terms
in expressions without the need of an explicit upcasting operator.
Note that these are the (infinite precision) mathematical integers, not the finite precision machine integers used in most programming languages. The latter are models by bit vector types.
x, y : INT; QUERY ((2 * x + 4 * y <= 1) AND ( y >= x)) => (x <= 0); z : REAL; QUERY (2 * x + z <= 3.5) AND (z >= 1);
Bit Vector Types
For every positive integer 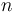 , the type
, the type 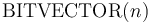 is interpreted as the set of all bit vectors of size
is interpreted as the set of all bit vectors of size 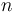 .
A rich set of bit vector operators is supported.
.
A rich set of bit vector operators is supported.
User-defined Basic Types
Users can define new basic types (often referred to as uninterpreted types in the SMT literature). Each such type is interpreted as a set of unspecified cardinality but disjoint from any other type. User-defined basic types are created by declarations like the following:
% User declarations of basic types: MyBrandNewType: TYPE; Apples, Oranges: TYPE;
Structured Types
CVC4's structured types are divided in the following families.
Array Types
Array types are created by the mixfix type constructors 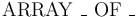 whose arguments can be instantiated by any value type.
whose arguments can be instantiated by any value type.
I : TYPE; %% Array types: % Arrays with indices from I and values from REAL Array1: TYPE = ARRAY I OF REAL; % Arrays with integer indices and array values Array2: TYPE = ARRAY INT OF (ARRAY INT OF REAL); % Arrays with integer pair indices and integer values IntMatrix: TYPE = ARRAY [INT, INT] OF INT;
An array type of the form 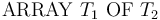 is interpreted
as the set of all total maps from
is interpreted
as the set of all total maps from 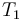 to
to 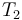 .
The main difference with the function type
.
The main difference with the function type 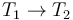 is that arrays,
contrary to functions, are first-class objects of the language, that is, values of an array
type can be arguments or results of functions.
Furthermore, array types come equipped with an update operation.
is that arrays,
contrary to functions, are first-class objects of the language, that is, values of an array
type can be arguments or results of functions.
Furthermore, array types come equipped with an update operation.
Tuple Types
Tuple types are created by the mixfix type constructors
![\begin{array}{l} [\ \_\ ] \\[1ex] [\ \_\ ,\ \_\ ] \\[1ex] [\ \_\ ,\ \_\ \ ,\ \_\ ] \\[1ex] \ldots \end{array}](/w/images/math/3/6/3/363b37d8100a693eb31d36831485ad6d.png)
whose arguments can be instantiated by any value type.
IntArray: TYPE = ARRAY INT OF INT; % Tuple type declarations RealPair: TYPE = [REAL, REAL] MyTuple: TYPE = [ REAL, IntArray, [INT, INT] ];
A tuple type of the form ![[T_1, \ldots, T_n]](/w/images/math/c/9/f/c9fba5c5df4d2385d01d4063e9ee86a9.png) is interpreted
as the Cartesian product
is interpreted
as the Cartesian product  .
.
Note that while the types 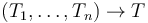 and
and
![[T_1 \times \cdots \times T_n] \to T](/w/images/math/5/e/7/5e7d9275ad22c39ef5ea9d44c1a45190.png) are semantically equivalent,
they are operationally different in CVC4.
The first is the type of functions that take
are semantically equivalent,
they are operationally different in CVC4.
The first is the type of functions that take 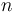 arguments
of respective type
arguments
of respective type 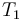 ,
,  ,
, 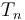 ,
while the second is the type of functions that take one argument of an
,
while the second is the type of functions that take one argument of an 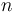 -tuple type.
-tuple type.
Record Types
Similar to, but more general than tuple types, record types are created by type constructors of the form
![[\#\ l_1: \_\ ,\ \ldots\ ,\ l_n: \_\ \#]](/w/images/math/5/1/c/51c734d9fa14b2fbe03f3eedaec9c036.png)
where 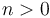 ,
,  are field labels,
and the arguments can be instantiated with any first-order types.
are field labels,
and the arguments can be instantiated with any first-order types.
MyType: TYPE; % Record declaration RecordType: TYPE = [# id: REAL, age: INT, info: MyType #];
The order of the fields in a record type is meaningful: permuting the field names gives a different type.
Note that record types are non-recursive.
For instance, it is not possible to declare a record type called Person containing
a field of type Person.
Recursive types are provided in CVC4 by the more general inductive data types.
(As a matter of fact, both record and tuple types are implemented internally as inductive data types.)
Inductive Data Types
Inductive data types in CVC4 are similar to inductive data types of functional languages. They can be parametric or not.
Non-Parametric Data Types
Non-parametric data types are created by declarations of the form
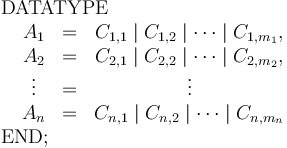
where
each 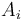 is a type name and
each
is a type name and
each 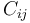 is either a constant symbol or an expression of the form
is either a constant symbol or an expression of the form
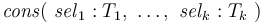
where  are any first-order types, including any
are any first-order types, including any 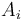 .
Such declarations define the data types
.
Such declarations define the data types  .
For each data type
.
For each data type 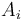 they introduce:
they introduce:
- constructor symbols
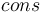 of type
of type 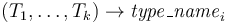 ,
, - selector symbols
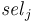 of type
of type 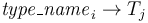 , and
, and - tester symbols
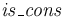 of type
of type 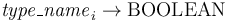 .
.
Note that permitting more than one data type to be defined in the same declarations allows the definition of mutually recursive types.
% simple enumeration type
% implicitly defined are the testers: is_red, is_yellow and is_blue
% (similarly for the other data types)
DATATYPE
PrimaryColor = red | yellow | blue
END;
% infinite set of pairwise distinct values ..., v(-1), v(0), v(1), ...
DATATYPE
Id = v (id: INT)
END;
% ML-style integer lists
DATATYPE
IntList = nil | ins (head: INT, tail: IntList)
END;
% AST for lamba calculus
DATATYPE
Term = var (index: INT)
| apply (arg_1: Term, arg_2: Term)
| lambda (arg: INT, body: Term)
END;
% Trees
DATATYPE
Tree = tree (value: REAL, children: TreeList),
TreeList = nil_tl
| ins_tl (first_t1: Tree, rest_t1: TreeList)
END;
Constructor, selector and tester symbols defined for a data type have global scope. So, for example, it is not possible for two different data types to use the same name for a constructor.
An inductive data type is interpreted as a term algebra constructed by the constructor symbols
over some sets of generators.
For example, the type IntList defined above is interpreted as the set
of all terms constructed with nil and ins over the integers.
Parametric Data Types
Parametric data types are infinite families of (non-parametric) data types with each family parametrized by one or more type variables. They are created by declarations of the form
![\begin{array}{l}
\mathrm{DATATYPE}\ [X_1, \ldots, X_p] \\
\begin{array}{ccc}
\ \ A_1 & = & C_{1,1} \mid C_{1,2} \mid \cdots \mid C_{1,m_1}, \\
\ \ A_2 & = & C_{2,1} \mid C_{2,2} \mid \cdots \mid C_{2,m_2}, \\
\ \ \vdots & = & \vdots \\
\ \ A_n & = & C_{n,1} \mid C_{n,2} \mid \cdots \mid C_{n,m_n} \\
\end{array}
\\
\mathrm{END};
\end{array}](/w/images/math/7/0/f/70f7e78878be16828da405a36f0f6675.png)
where
 are type variables,
each
are type variables,
each 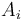 is a type name parametrized by some of the variables
is a type name parametrized by some of the variables  and
each
and
each 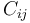 is either a constant symbol or an expression of the form
is either a constant symbol or an expression of the form
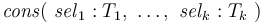
where  are any first-order types,
possibly parametrized by
are any first-order types,
possibly parametrized by  , including any
, including any 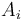 .
.
% Parametric pairs DATATYPE [X, Y] Pair[X, Y] = pair (first: X, second: Y) END; % Parametric lists DATATYPE [X] List[X] = nil | cons (head: X, tail: List[X]) END; % Parametric trees using the list type above DATATYPE [X] Tree[X] = node (value: X, children: List[Tree[X]]), END;
The declarations above define infinitely many types of the form
Pair[S,T], List[T] and Tree[T] where S and T are first-order types.
Note that the identifier List above, for example, by itself does not denote a type.
In contrast, the terms List[Real], List[List[Real]], List[Tree[INT]],
and so on do.
Restriction to Inductive Types
By adopting a term algebra semantics, CVC4 allows only inductive data types, that is, data types whose values are essentially (labeled, ordered) finite trees. Infinite structures such as streams or even finite but cyclic ones such as circular lists are then excluded. For instance, none of the following declarations define inductive data types, and are rejected by CVC4:
DATATYPE
IntStream = s (first:INT, rest: IntStream)
END;
DATATYPE
RationalTree = node1 (child: RationalTree)
| node2 (left_child: RationalTree, right_child:RationalTree)
END;
DATATYPE
T1 = c1 (s1: T2),
T2 = c2 (s2: T1)
END;
In concrete, a declaration of 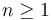 datatypes
datatypes  will be rejected if for any one of the types
will be rejected if for any one of the types  , it is impossible to build a finite term of that type using only the constructors of
, it is impossible to build a finite term of that type using only the constructors of  and free constants of type other than
and free constants of type other than  .
.
Inductive data types are the only types where the user also chooses names for the built-in operations to:
- construct a value of the type (with the constructors),
- extract components from a value (with the selectors), or
- check if a value was constructed with a certain constructor or not (with the testers).
For all the other types, CVC4 provides predefined names for the built-in operations on the type.
Function Types
Function ( ) types are created by the mixfix type constructors
) types are created by the mixfix type constructors
![\begin{array}{l}
\_ \to \_ \\[1ex] (\ \_\ ,\ \_\ ) \to \_
\\[1ex] (\ \_\ ,\ \_\ ,\ \_\ ) \to \_
\\[1ex] \ldots
\end{array}](/w/images/math/f/0/5/f05367bbd89f32c4ca754b620c82f158.png)
whose arguments can be instantiated by any first-order type.
% Function type declarations UnaryFunType: TYPE = INT -> REAL; BinaryFunType: TYPE = (REAL, REAL) -> ARRAY REAL OF REAL; TernaryFunType: TYPE = (REAL, BITVECTOR(4), INT) -> BOOLEAN;
A function type of the form 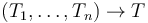 with
with 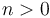 is interpreted as the set of all total functions from the Cartesian product
is interpreted as the set of all total functions from the Cartesian product  to
to 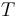 .
.
The example above also shows how to introduce type names.
A name like UnaryFunType above is just an abbreviation for the type 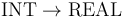 and can be used interchangeably with it.
and can be used interchangeably with it.
In general, any type defined by a type expression E can be given a name with the declaration:
name : TYPE = E;
Type Checking
In CVC4, formulas and terms are statically typed at the level of types
(as opposed to subtypes) according to the usual rules of first-order many-sorted logic,
with the main difference that formulas are just terms of type 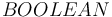 :
:
- each variable has one associated first-order type,
- each constant symbol has one or more associated first-order types,
- each function symbol has one or more associated function types,
- the type of a term consisting just of a variable is the type associated to that variable,
- the type of a term consisting just of a constant symbol is the type associated to that constant symbol,
- the term obtained by applying a function symbol
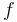 to the terms
to the terms  is
is 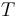 if
if 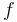 has type
has type 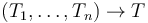 and each
and each 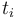 has type
has type 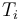 .
.
Attempting to enter an ill-typed term will result in an error.
Another significant difference with standard many-sorted logic is that
some built-in symbols are parametrically polymorphic.
For instance, the function symbol for extracting the element of any array has
type 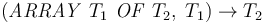 for all first-order types
for all first-order types 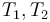 .
.
Type Ascription
By the type inference rules above some terms might have more than one type.
This can happen with terms built with polymorphic data type constructors
that have more than one return type for the same input type.
In that case, a type ascription operator (::) must be applied
to the constructor to specify the intended return type.
DATATYPE [X] List[X] = nil | cons (head: X, tail: List[X]) END; ASSERT y = cons(1, nil::List[REAL]); DATATYPE [X, Y] Union[X, Y] = left(val_l: X) | right(val_r: Y) END; ASSERT y = left::Union[BOOLEAN, REAL](TRUE);
The constant symbol 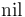 declared above has infinitely many types
(
declared above has infinitely many types
(![\mathrm{List}[\mathrm{REAL}]](/w/images/math/2/d/1/2d16f38725189013d5de469f1d61410c.png) ,
, ![\mathrm{List}[\mathrm{BOOLEAN}]](/w/images/math/9/4/b/94b40c9bef740d73ce1476fe36e20642.png) ,
,
![\mathrm{List}[[\mathrm{REAL}, \mathrm{REAL}]]](/w/images/math/0/a/d/0ad9ef6e5b4f5c64470741488fead040.png) ,
,
![\mathrm{List}[\mathrm{List}[\mathrm{REAL}]]](/w/images/math/5/b/3/5b3b5042c240d165d3a6a70524bb99c9.png) , ...)
CVC4's type checker requires the user to indicate explicitly the type
of each occurrence of
, ...)
CVC4's type checker requires the user to indicate explicitly the type
of each occurrence of nil in a term.
Similarly,
the injection operator left has infinitely many return types
for the same input type, for instance:
![\mathrm{BOOLEAN} \to \mathrm{Union}[\mathrm{BOOLEAN}, \mathrm{REAL}]](/w/images/math/f/f/8/ff835defb13072f3fb1232c0064fe7e7.png) ,
,
![\mathrm{BOOLEAN} \to \mathrm{Union}[\mathrm{BOOLEAN}, [\mathrm{REAL}, \mathrm{REAL}]]](/w/images/math/e/d/7/ed7d8d26e627cc89cb7c03830b717d11.png) ,
,
![\mathrm{BOOLEAN} \to \mathrm{Union}[\mathrm{BOOLEAN}, \mathrm{List}[\mathrm{REAL}]]](/w/images/math/f/8/2/f8280251cb3d7261fdcba998a4ffb6cd.png) ,
and so on.
Applications of
,
and so on.
Applications of left need to specify the intended returned typed, as shown above.
Terms and Formulas
In addition to type expressions, CVC4 has expressions for terms and for formulas
(i.e., terms of type 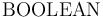 ).
By and large, these are standard first-order terms built out of typed variables,
predefined theory-specific operators, free (i.e., user-defined) function symbols,
and quantifiers.
Extensions include an if-then-else operator, lambda abstractions, and local symbol
declarations, as illustrated below.
Note that these extensions still keep CVC4's language first-order.
In particular, lambda abstractions are restricted to take and return only terms of
a first-order type.
Similarly, variables can only be of a first-order type.
).
By and large, these are standard first-order terms built out of typed variables,
predefined theory-specific operators, free (i.e., user-defined) function symbols,
and quantifiers.
Extensions include an if-then-else operator, lambda abstractions, and local symbol
declarations, as illustrated below.
Note that these extensions still keep CVC4's language first-order.
In particular, lambda abstractions are restricted to take and return only terms of
a first-order type.
Similarly, variables can only be of a first-order type.
A number of built-in function symbols (for instance, the arithmetic ones) are used as infix operators. All user-defined symbols are used as prefix ones.
User-defined, i.e., free, function symbols include constant symbols and
predicate symbols, respectively nullary function symbols and function symbols
with a 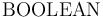 return type.
These symbols are introduced with global declarations of the form
return type.
These symbols are introduced with global declarations of the form
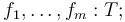 where
where 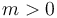 ,
, 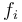 are the names of the symbols and
are the names of the symbols and
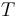 is their type:
is their type:
% integer constants a, b, c: INT; % real constants x, y, z: REAL; % unary function f1: REAL -> REAL; % binary function f2: (REAL, INT) -> REAL; % unary function with a tuple argument f3: [INT, REAL] -> BOOLEAN; % binary predicate p: (INT, REAL) -> BOOLEAN; % Propositional "variables" P, Q; BOOLEAN;
Like type declarations, function symbol declarations like the above have global scope and must be unique. In other words, it is not possible to declare a function symbol globally more than once in the same lexical scope. This entails among other things that globally-defined free symbols cannot be overloaded with different types and that theory symbols cannot be redeclared globally as free symbols.
Global symbol definitions
As with types, a function symbol can be defined as the name of another term
of the corresponding type.
With constant symbols, this is done with a declaration of the form 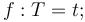 :
:
c: INT; i: INT = 5 + 3*c; % i is effectively a shorthand for 5 + 3*c j: REAL = 3/4; t: [REAL, INT] = (2/3, -4); r: [# key: INT, value: REAL #] = (# key := 4, value := (c + 1)/2 #); f: BOOLEAN = FORALL (x:INT): x <= 0 OR x > c ;
A restriction on constants of type 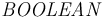 is that their value
can only be a closed formula, that is, a formula with no free variables.
is that their value
can only be a closed formula, that is, a formula with no free variables.
A term and its name can be used interchangeably in later expressions. Named terms are often useful for shared subterms (terms used several times in different places) since their use can make the input exponentially more concise. Named terms are processed very efficiently by CVC4. It is much more efficient to associate a complex term with a name directly rather than to declare a constant and later assert that it is equal to the same term. This point is explained in more detail later in section Commands.
More generally, in CVC4 one can associate a term to function symbols of any arity. For non-constant function symbols this is done with a declaration of the form
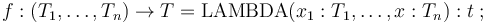
where 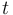 is any term of type
is any term of type 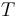 with free variables
in
with free variables
in  .
The lambda binder has the usual semantics and conforms to the usual lexical scoping rules:
within the term
.
The lambda binder has the usual semantics and conforms to the usual lexical scoping rules:
within the term 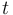 the declaration of the symbols
the declaration of the symbols  as local variables of respective type
as local variables of respective type  hides any previous
declarations of those symbols that are in scope.
hides any previous
declarations of those symbols that are in scope.
As a general shorthand, when 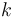 consecutive types
consecutive types
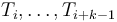 in the lambda expression
in the lambda expression
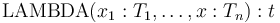 are identical, the syntax
are identical, the syntax
 can also be used.
can also be used.
% Global declaration of x as a unary function symbol x: REAL -> REAL; % Local declarations of x as variable (hiding the global one) f: REAL -> REAL = LAMBDA (x: REAL): 2*x + 3; p: (INT, INT) -> BOOLEAN = LAMBDA (x,i: INT): i*x - 1 > 0; g: (REAL, INT) -> [REAL, INT] = LAMBDA (x: REAL, i:INT): (x + 1, i - 3);
Note that lambda definitions are not recursive:
the symbol being defined cannot occur in the body of the lambda term.
They should be understood as macros.
For instance, any occurrence of the term 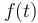 where
where 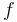 is as defined above will be treated
as if it was the term
is as defined above will be treated
as if it was the term 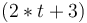 .
.
Local symbol definitions
Constant and function symbols can also be declared locally anywhere within a term by means of a let binder. This is done with a declaration of the form
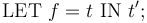
where 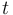 is a term with no free variables, possibly a lambda term.
Let binders can be nested arbitrarily and follow the usual lexical scoping rules.
The following general form
is a term with no free variables, possibly a lambda term.
Let binders can be nested arbitrarily and follow the usual lexical scoping rules.
The following general form
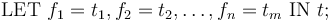
can be use above can used as a shorthand for
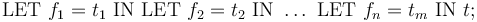
t: REAL =
LET x1 = 42,
g = LAMBDA(x:INT): x + 1,
x2 = 2*x1 + 7/2
IN
(LET x3 = g(x1) IN x3 + x2) / x1;
Note that the same symbol = is used, unambiguously, in the syntax of global declarations, let declarations, and as a predicate symbol.
Note:
A 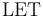 term with a multiple symbols defines them sequentially.
A parallel version of the
term with a multiple symbols defines them sequentially.
A parallel version of the 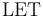 construct will be introduced in a later version.
construct will be introduced in a later version.
Built-in theories and their symbols
In addition to user-defined symbols, CVC4 terms can use a number of predefined symbols:
the logical symbols, such as 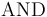 ,
, 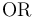 , etc.,
as well as theory symbols, function symbols belonging to one of the built-in theories.
They are described next, with the theory symbols grouped by theory.
, etc.,
as well as theory symbols, function symbols belonging to one of the built-in theories.
They are described next, with the theory symbols grouped by theory.
Logical Symbols
The logical symbols in CVC4's language include
the equality and disequality predicate symbols, respectively written as = and /=,
the multiarity disequality symbol 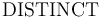 ,
together with the logical constants
,
together with the logical constants 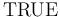 ,
, 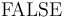 ,
the connectives
,
the connectives 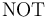 ,
, 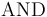 ,
, 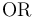 ,
, 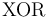 ,
,  ,
,  , and
the first-order quantifiers
, and
the first-order quantifiers 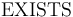 and
and 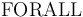 ,
all with the standard many-sorted logic semantics.
,
all with the standard many-sorted logic semantics.
The binary connectives have infix syntax and type
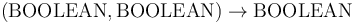 .
The symbols = and /=, which are also infix, are instead parametrically polymorphic,
having type
.
The symbols = and /=, which are also infix, are instead parametrically polymorphic,
having type 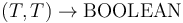 for every first-order type
for every first-order type 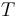 .
They are interpreted respectively as the identity relation and its complement.
.
They are interpreted respectively as the identity relation and its complement.
The DISTINCT symbol is both overloaded and polymorphic.
It has type 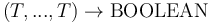 for every sequence
for every sequence 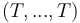 of length
of length 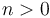 and first-order type
and first-order type 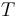 .
For each
.
For each 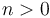 , it is interpreted as the relation
that holds exactly for tuples of pairwise distinct elements.
, it is interpreted as the relation
that holds exactly for tuples of pairwise distinct elements.
The syntax for quantifiers is similar to that of the lambda binder.
Here is an example of a formula built just of these logical symbols and variables:
A, B: TYPE;
q: BOOLEAN = FORALL (x,y: A, i,j,k: B):
i = j AND i /= k => EXISTS (z: A): x /= z OR z /= y;
Binding and scoping of quantified variables follows the same rules as in let expressions. In particular, a quantifier will shadow in its scope any constant and function symbols with the same name as one of the variables it quantifies:
A: TYPE; i, j: INT; % The first occurrence of i and of j in f are constant symbols, % the others are variables. f: BOOLEAN = i = j AND FORALL (i,j: A): i = j OR i /= j;
Optionally, it is also possible to specify instantiation patterns
for quantified variables.
The general syntax for a quantified formula 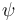 with patterns is
with patterns is
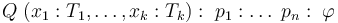
where 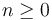 ,
, 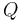 is
either
is
either 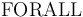 or
or 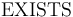 ,
,
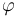 is a term of type
is a term of type 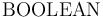 ,
and each of the
,
and each of the 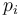 's,
a pattern for the quantifier
's,
a pattern for the quantifier 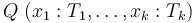 , has the form
, has the form
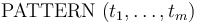
where  and
and  are
arbitrary binder-free terms (no lets, no quantifiers).
Those terms can contain (free) variables, typically, but not exclusively,
drawn from
are
arbitrary binder-free terms (no lets, no quantifiers).
Those terms can contain (free) variables, typically, but not exclusively,
drawn from  .
(Additional variables can occur if
.
(Additional variables can occur if  occurs in a bigger formula
binding those variables.)
occurs in a bigger formula
binding those variables.)
A: TYPE;
b, c: A;
p, q: A -> BOOLEAN;
r: (A, A) -> BOOLEAN;
ASSERT FORALL (x0, x1, x2: A):
PATTERN (r(x0, x1), r(x1, x2)):
(r(x0, x1) AND r(x1, x2)) => r(x0, x2) ;
ASSERT FORALL (x: A):
PATTERN (r(x, b)):
PATTERN (r(x, c)):
p(x) => q(x) ;
ASSERT EXISTS (y: A):
FORALL (x: A):
PATTERN (r(x, y), p(y)):
r(x, y) => q(x) ;
Patterns have no logical meaning: adding them to a formula does not change its semantics. Their purpose is purely operational, as explained in the Instantiation Patterns section.
In addition to these constructs, CVC4 also has a general mixfix conditional operator of the form
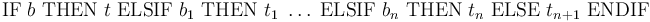
with 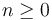 where
where
 are terms of type
are terms of type 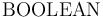 and
and
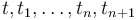 are terms of the same first-order type
are terms of the same first-order type 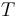 :
:
% Conditional term x, y, z, w: REAL; t: REAL = IF x > 0 THEN y ELSIF x >= 1 THEN z ELSIF x > 2 THEN w ELSE 2/3 ENDIF;
User-defined Functions and Types
The theory of user-defined functions,also know in the SMT literature as the theory Equality over Uninterpreted Functions, or EUF, is in effect a family of theories of equality parametrized by the basic types and the free symbols a user can define during a run of CVC4.
This theory has no built-in symbols (other than the logical ones). Its types consist of all and only the user-defined types. Its function symbols consist of all and only the user-defined free symbols.
Arithmetic
The real arithmetic theory has two types:
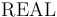 and
and 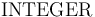 with the latter a subtype of the first.
Its built-in symbols for the usual arithmetic constants
and operators over the type
with the latter a subtype of the first.
Its built-in symbols for the usual arithmetic constants
and operators over the type 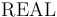 , each with the expected type:
all numerals 0, 1, ..., as well as - (both unary and binary), +, *, /, <, >, <=, >=.
Application of the binary symbols are in infix form.
, each with the expected type:
all numerals 0, 1, ..., as well as - (both unary and binary), +, *, /, <, >, <=, >=.
Application of the binary symbols are in infix form.
Rational values can be expressed in decimal or fractional format: e.g., 0.1, 23.243241, 1/2, 3/4, and so on. A leading 0 is mandatory for decimal numbers smaller than one (e.g., the syntax .3, say, is cannot be used as a shorthand for 0.3). The size of the numerals used in the representation of natural and rational numbers is unbounded; more accurately, bounded only by the amount of available memory.
Bit vectors
Arrays
The theory of arrays is a parametric theory of (total) unary maps. It comes equipped with mixfix polymorphic selection and update operators, respectively
![\_[\_]](/w/images/math/4/a/2/4a2e18f55a77d1837ef34ba945085e81.png) and
and ![\_\ \mathrm{WITH}\ [\_]\ := \_](/w/images/math/b/a/1/ba1c75187dd461efe773b6e869cd0ba7.png) .
.
The semantics of these operators is the expected one:
for all first-order types  and
and 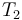 ,
if
,
if 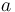 is of type
is of type 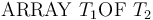 ,
,
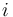 is of type
is of type 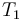 , and
, and
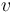 is of type
is of type 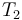 ,
,
-
![a[i]](/w/images/math/5/9/5/595711c58954cfc2eb727cba561e3512.png) denotes the value that
denotes the value that 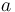 associates to index
associates to index 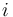 ,
, -
![a\ \mathrm{WITH}\ [i]\ := v](/w/images/math/d/7/f/d7f9d1a4db09b9e1cf83ec5805394e65.png) denotes a map that associates
denotes a map that associates 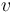 to index
to index 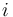 and is otherwise identical to
and is otherwise identical to 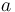 .
.
Sequential updates can be chained with the shorthand syntax
![\_\ \mathrm{WITH}\ [\_]\ := \_, \ldots, [\_]\ := \_](/w/images/math/9/6/0/9607705d830a35d96751ffcd1d491fd5.png) .
.
A: TYPE = ARRAY INT OF REAL; a: A; i: INT = 4; % selection: elem: REAL = a[i]; % update a1: A = a WITH [10] := 1/2; % sequential update % (syntactic sugar for (a WITH [10] := 2/3) WITH [42] := 3/2) a2: A = a WITH [10] := 2/3, [42] := 3/2;
Since arrays are just maps, equality between them is extensional, that is, for two arrays of the same type to be different they have to map at least one index to differ values.
Data types
The theory of inductive data types is in fact a family of theories parametrized by a data type declaration specifying constructors and selectors for one or more user-defined data types.
No built-in operators other than equality and disequality are provided for this family in the native language. Each user-provided data type declaration, however, generates constructor, selector and tester operators as described in the Inductive Data Types section.
Tuples and Records
Semantically both records and tuples can be seen as special instances
of inductive data types.
CVC4 implements them internally indeed as data types.
In essence, a record type ![[\#\ l_0:T_0, \ldots, l_n:T_n\ \#]](/w/images/math/d/3/2/d32254e7016873239bd2e36120e7e544.png) is encoded as a data type of the form
is encoded as a data type of the form
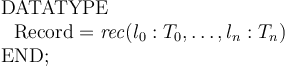
Tuples of length 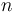 are in turn special cases of records whose field names are
the numerals from
are in turn special cases of records whose field names are
the numerals from 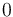 to
to 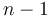 .
.
Externally, tuples and records have their own syntax for constructor and selector operators.
- Records of type
![[\#\ l_0:T_0, \ldots, l_n:T_n\ \#]](/w/images/math/d/3/2/d32254e7016873239bd2e36120e7e544.png) have the associated record constructor
have the associated record constructor  whose arguments must be terms of type
whose arguments must be terms of type  , respectively.
, respectively. - Tuples of type
![[\ T_0, \ldots, T_n\ ]](/w/images/math/5/4/7/547c8eb765415544e64bc4c77519e72e.png) have the associated tuple constructor
have the associated tuple constructor  whose arguments must be terms of type
whose arguments must be terms of type  , respectively.
, respectively.
The selector operators on records and tuples follows a dot notation syntax.
% Record construction and field selection Item: TYPE = [# key: INT, weight: REAL #]; x: Item = (# key := 23, weight := 43/10 #); k: INT = x.key; v: REAL = x.weight; % Tuple construction and projection y: [REAL, INT, REAL] = ( 4/5, 9, 11/9 ); first_elem: REAL = y.0; third_elem: REAL = y.2;
Differently from data types, records and tuples are also provided with built-in update operators similar in syntax and semantics to the update operator for arrays.
More precisely, for each record type ![[\#\ l_0:T_0, \ldots, l_n:T_n\ \#]](/w/images/math/d/3/2/d32254e7016873239bd2e36120e7e544.png) and
each
and
each 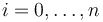 , CVC4 provides the operator
, CVC4 provides the operator
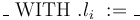
The operator maps a record 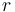 of that type and a value
of that type and a value 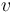 of type
of type 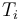 to the record that stores
to the record that stores 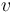 in field
in field 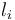 and is otherwise identical to
and is otherwise identical to 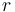 .
Analogously, for each tuple type
.
Analogously, for each tuple type ![[T_0, \ldots, T_n]](/w/images/math/e/7/c/e7c044c5044f03caae7f99e5a699a069.png) and
each
and
each 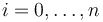 , CVC4 provides the operator
, CVC4 provides the operator
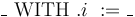
with similar semantics.
% Record updates Item: TYPE = [# key: INT, weight: REAL #]; x: Item = (# key := 23, weight := 43/10 #); x1: Item = x WITH .weight := 48; % Tuple updates Tup: TYPE = [REAL,INT,REAL]; y: Tup = ( 4/5, 9, 11/9 ); y1: Tup = y WITH .1 := 3; Updates to a nested component can be combined in a single WITH operator: Cache: TYPE = ARRAY [0..100] OF [# addr: INT, data: REAL #]; State: TYPE = [# pc: INT, cache: Cache #]; s0: State; s1: State = s0 WITH .cache[10].data := 2/3;
Note that, differently from updates on arrays, tuple and record updates are
just additional syntactic sugar.
For instance, the record x1 and tuple y1 defined above
could have been equivalently defined as follows:
% Record updates Item: TYPE = [# key: INT, weight: REAL #]; x: Item = (# key := 23, weight := 43/10 #); x1: Item = (# key := x.key, weight := 48 #); % Tuple updates Tup: TYPE = [REAL,INT,REAL]; y: Tup = ( 4/5, 9, 11/9 ); y1: Tup = ( y.0, 3, y.1 );
Commands
In addition to declarations of types and function symbols, the CVC4 native language contains the following commands:
-
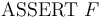 -- Add the formula
-- Add the formula 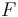 to the current logical context
to the current logical context 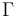 .
. -
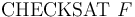 -- Check if the formula
-- Check if the formula 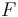 is satisfiable in the current logical context (
is satisfiable in the current logical context (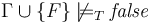 ).
).
-
 -- After an invalid
-- After an invalid 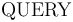 or satisfiable
or satisfiable 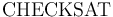 , search for a counter-example different from the current one.
, search for a counter-example different from the current one. -
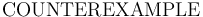 -- After an invalid
-- After an invalid  or satisfiable
or satisfiable  , print the context that is a witness for invalidity/satisfiability.
, print the context that is a witness for invalidity/satisfiability. -
 -- After an invalid
-- After an invalid  or satisfiable
or satisfiable 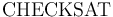 , print a model that makes the formula invalid/satisfiable. The model is provided in terms of concrete values for each free symbol.
, print a model that makes the formula invalid/satisfiable. The model is provided in terms of concrete values for each free symbol. -
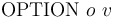 -- Set the command-line option flag
-- Set the command-line option flag  to value
to value  . The argument
. The argument 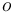 is provide as a string literal enclosed in double-quotes and
is provide as a string literal enclosed in double-quotes and 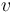 as an integer value.
as an integer value. -
 -- Equivalent to
-- Equivalent to 
-
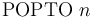 -- Restore the system to the state it was in right before the most recent call to
-- Restore the system to the state it was in right before the most recent call to 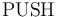 made from stack level
made from stack level 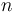 . Note that the current stack level is printed as part of the output of the
. Note that the current stack level is printed as part of the output of the  command.
command. -
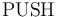 -- Save (checkpoint) the current state of the system.
-- Save (checkpoint) the current state of the system. -
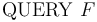 -- Check if the formula
-- Check if the formula 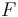 is valid in the current logical context (
is valid in the current logical context (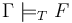 ).
). -
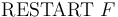 -- After an invalid
-- After an invalid 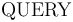 or satisfiable
or satisfiable 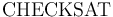 , repeat the check but with the additional assumption
, repeat the check but with the additional assumption 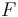 in the context.
in the context. -
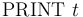 -- Parse and print back the term
-- Parse and print back the term 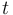 .
. -
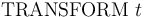 -- Simplify the term
-- Simplify the term 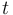 and print the result.
and print the result. -
 -- Print all the formulas in the current logical context
-- Print all the formulas in the current logical context 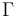 .
.
The remaining commands take a single argument, given as a string literal enclosed in double-quotes.
-
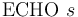 -- Print string
-- Print string 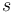
-
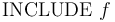 -- Read commands from file
-- Read commands from file 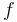 .
. -
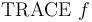 -- Turn on tracing for the debug flag
-- Turn on tracing for the debug flag 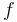 .
. -
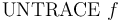 -- Turn off tracing for the debug flag
-- Turn off tracing for the debug flag 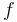 .
.
Here, we explain some of the above commands in more detail.
QUERY
The command 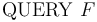 invokes the core functionality of CVC4 to check
the validity of the formula
invokes the core functionality of CVC4 to check
the validity of the formula 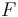 with respect to the assertions made thus far,
which constitute the context
with respect to the assertions made thus far,
which constitute the context 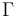 .
The argument
.
The argument 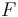 must be well typed term of type
must be well typed term of type 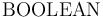 ,
as described in Terms and Formulas.
,
as described in Terms and Formulas.
The execution of this command always terminates and produces one of three possible answers:
Valid, Invalid, and Unknown.
- A
Validanswer indicates that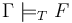 . After a query returning such an answer, the logical context
. After a query returning such an answer, the logical context 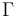 is exactly as it was before the query.
is exactly as it was before the query. - An
Invalidanswer indicates that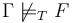 , that is, there is a model of the background theory
, that is, there is a model of the background theory 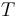 that satisfies
that satisfies 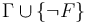 . When
. When 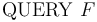 returns
returns Invalid, the logical context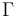 is augmented with a set
is augmented with a set  of ground (i.e., variable-free) literals such that
of ground (i.e., variable-free) literals such that 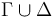 is satisfiable in
is satisfiable in 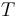 , but
, but 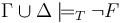 . In fact, in this case
. In fact, in this case  propositionally entails
propositionally entails 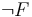 , in the sense that, every truth assignment to the literals of
, in the sense that, every truth assignment to the literals of  that satisfies
that satisfies  falsifies
falsifies 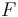 . We call the new context
. We call the new context 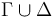 a counterexample for
a counterexample for 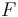 .
. - An
Unknownanswer is similar to anInvalidanswer in that additional literals are added to the context which propositionally entail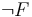 . The difference in this case is that CVC4 cannot guarantee that
. The difference in this case is that CVC4 cannot guarantee that 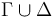 is actually satisfiable in
is actually satisfiable in 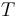 .
.
CVC4 may report Unknown when the context or the query contains
non-linear arithmetic terms or quantifiers.
In all other cases, it is expected to be sound and complete,
i.e., to report Valid if 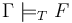 and
and Invalid otherwise.
After an Invalid (resp. Unknown) answer,
counterexamples (resp. possible counterexamples) can be obtained with
a  ,
,  ,
or
,
or  command.
command.
Since the  command may modify
the current context, if one needs to check several formulas in a row
in the same context, it is a good idea to surround every
query by a
command may modify
the current context, if one needs to check several formulas in a row
in the same context, it is a good idea to surround every
query by a  and
and  invocation
in order to preserve the context:
invocation
in order to preserve the context:
PUSH; QUERY <formula>; POP;
CHECKSAT
RESTART
Instantiation Patterns
CVC4's support for the SMT-LIB language
SMT-LIB compliance
Every effort has been made to make CVC4 compliant with the SMT-LIB 2.0 standard (http://smtlib.org/). However, when parsing SMT-LIB input, certain default settings don't match what is stated in the official standard. To make CVC4 adhere more strictly to the standard, use the "--smtlib" command-line option. Even with this setting, CVC4 is somewhat lenient; some non-conforming input may still be parsed and processed.
The CVC4 library interface (API)
Using CVC4 in a C++ project
Using CVC4 from Java
The compatibility interface
Upgrading from CVC3 to CVC4
Features not supported by CVC4 (yet)
Type Correctness Conditions (TCCs)
Type Correctness Conditions (TCCs), and the checking of such, are not supported by CVC4 1.0. Thus, a function defined only on integers can be applied to REAL (as INT is a subtype of REAL), and CVC4 will not complain, but may produce strange results. For example:
f : INT -> INT; ASSERT f(1/3) = 0; ASSERT f(2/3) = 1; CHECKSAT; % sat COUNTEREXAMPLE; % f : (INT) -> INT = LAMBDA(x1:INT) : 0;
CVC3 can be used to produce TCCs for this input (with the +dump-tcc option). The TCC can be checked by CVC3 or another solver. (CVC3 can also check TCCs while solving with +tcc.)
If you were using the text interfaces of CVC3
The native language of all solvers in the CVC family, referred to as the "presentation language," has undergone some revisions for CVC4. The most notable is that CVC4 does _not_ add counterexample assertions to the current assertion set after a SAT/INVALID result. For example:
x, y : INT; ASSERT x = 1 OR x = 2; ASSERT y = 1 OR y = 2; ASSERT x /= y; CHECKSAT; % sat QUERY x = 1; % invalid QUERY x = 2; % invalid
Here, CVC4 responds "invalid" to the second and third queries, because each has a counterexample (x=2 is a counterexample to the first, and x=1 is a counterexample to the second). However, CVC3 will respond with "valid" to one of these two, as the first query (the CHECKSAT) had the side-effect of locking CVC3 into one of the two cases; the later queries are effectively querying the counterexample that was found by the first. CVC4 removes this side-effect of the CHECKSAT and QUERY commands.
CVC4 supports rational literals (of type REAL) in decimal; CVC3 did not support decimals.
CVC4 does not have support for the IS_INTEGER predicate.
If you were using the library ("in-memory") interface of CVC3
If you were using CVC3 from C
If you were using CVC3 from Java
Useful command-line options
Statistics
Statistics can be dumped on exit (both normal and abnormal exits) with the --statistics command line option.
Time and resource limits
CVC4 can be made to self-timeout after a given number of milliseconds. Use the --tlimit command line option to limit the entire run of CVC4, or use --tlimit-per to limit each individual query separately. Preprocessing time is not counted by the time limit, so for some large inputs which require aggressive preprocessing, you may notice that --tlimit does not work very well. If you suspect this might be the case, you can use "-vv" (double verbosity) to see what CVC4 is doing.
Time-limited runs are not deterministic; two consecutive runs with the same time limit might produce different results (i.e., one may time out and responds with "unknown", while the other completes and provides an answer). To ensure that results are reproducible, use --rlimit or --rlimit-per. These options take a "resource count" (presently, based on the number of SAT conflicts) that limits the search time. A word of caution, though: there is no guarantee that runs of different versions of CVC4 or of different builds of CVC4 (e.g., two CVC4 binaries with different features enabled, or for different architectures) will interpret the resource count in the same manner.
CVC4 does not presently have a way to limit its memory use; you may opt to run it from a shell after using "ulimit" to limit the size of the heap.
Dumping API calls or preprocessed output
Changing the output language
Proof support
CVC4 1.0 has limited support for proofs, and they are disabled by default. (Run the configure script with --enable-proof to enable proofs). Proofs are exported in LFSC format and are limited to the propositional backbone of the discovered proof (theory lemmas are stated without proof in this release).
Portfolio solving
If enabled at configure-time (./configure --with-portfolio), a second CVC4 binary will be produced ("pcvc4"). This binary has support for running multiple instances of CVC4 in different threads. Use --threads=N to specify the number of threads, and use --thread0="options for thread 0" --thread1="options for thread 1", etc., to specify a configuration for the threads. Lemmas are *not* shared between the threads by default; to adjust this, use the --filter-lemma-length=N option to share lemmas of N literals (or smaller). (Some lemmas are ineligible for sharing because they include literals that are "local" to one thread.)
Currently, the portfolio **does not work** with quantifiers or with the theory of inductive datatypes. These limitations will be addressed in a future release.
Emacs support
For a suggestion of editing CVC4 source code with emacs, see the file contrib/editing-with-emacs. For a CVC language mode (the native input language for CVC4), see contrib/cvc-mode.el.
